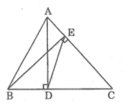
cho tam giác ABC có đường cao AD,BE.Chứng minh tam giác DEC đồng dạng tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NY
0
CM
24 tháng 12 2018
Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: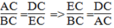
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
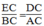
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
15 tháng 4 2022
a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)
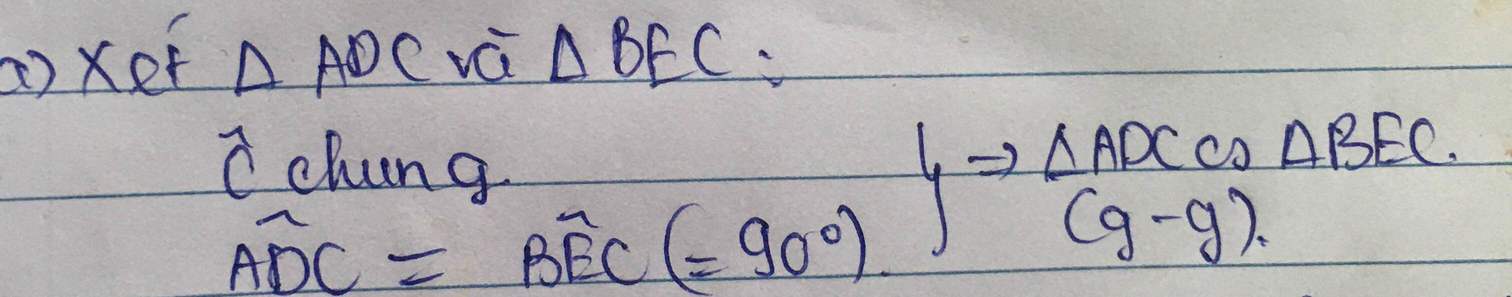
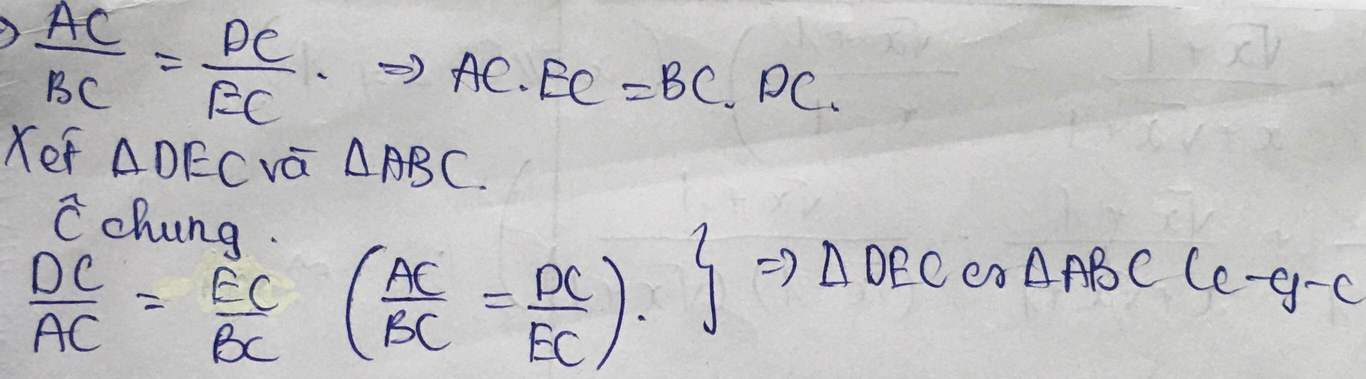
nhanh lên mình tích cko