cho tam giác abc cân tại a. TRên tia đối tia cb và bc lấy lần lượt e và d sao cho bd=ce.
a, CM; tam giác ADE cân
b, gọi m là trung điểm của bc.CM: AM là tia phân giác của góc DAE
c . BH vuông góc với AD. CK vuông góc với AE. CM: BH=CK
d CM: ba đường thẳng AM,BH,CK cùng đi qua 1 điểm

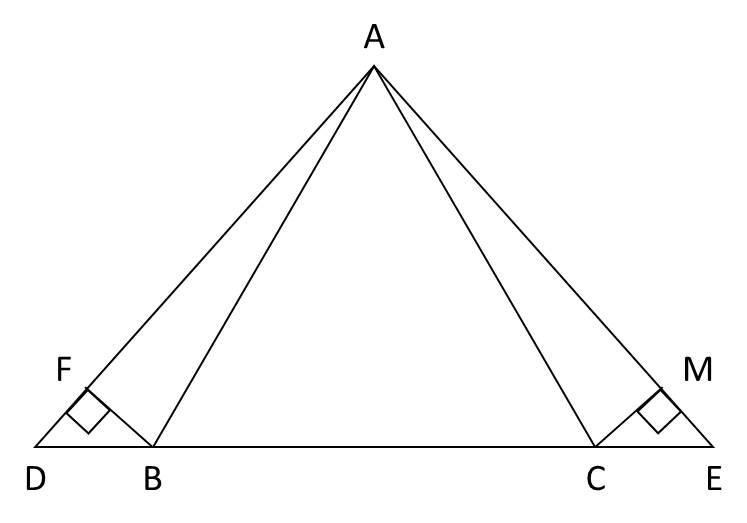
Em mời có lớp 5 thôi