chứng minh rằng tổng của n số tự nhiên lẻ liên tiếp (kể từ 1) là số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1
7 tháng 10 2018
Khoảng cách giữa 2 số lẻ liên tiếp là 2
Số lẻ đầu tiên là 1 thì số lẻ thứ n là:
\(1+\left(n-1\right).2=2n-1\)
Khi đó: tổng n STN lẻ liên tiếp kể từ 1 là:
\(1+3+5+...+\left(2n-1\right)\)
\(=\left(1+2n-1\right).n:2\)
\(=2n^2:2=n^2\)
Vậy tổng của n STN lẻ liên tiếp là số chính phương.
Chúc em học tốt.
PX
0
HT
2 tháng 7 2021
2.
Gọi x;x+1;x+2;x+3 là 4 số tự nhiên liên tiếp ( x\(\in\) N)
Ta có : x (x+1) (x+2 ) (x+3 ) +1
=( x2 + 3x ) (x2 + 2x + x +2 ) +1
= ( x2 + 3x ) (x2 +3x + 2 ) +1 (*)
Đặt t = x2 + 3x thì (* ) = t ( t+2 ) + 1= t2 + 2t +1 = (t+1)2 = (x2 + 3x + 1 )2
=> x (x+1) (x+2 ) (x+3 ) +1 là số chính phương
hay tích 4 số tự nhiên liên tiếp cộng 1 là số chính phương
TT
14 tháng 8 2020
Đề bài : Chứng minh rằng tổng lập phương của các số tự nhiên liên tiếp từ 1 đến n bằng bình phương của tổng từ 1 đến n ( n tự nhiên ). Hay ta cần chứng minh : \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) (*)
Lời giải :
+) Xét \(n=1\) thì ta có : \(1^3=1^2\) ( đúng )
Suy ra (*) đúng với \(n=1\) (1)
+) Xét \(n=2\) ta có : \(1^3+2^3=1+8=9\); \(\left(1+2\right)^2=3^2=9\)
\(\Rightarrow1^3+2^3=\left(1+2\right)^2\) ( đúng ). Nên (*) đúng với \(n=2\) (2)
+) Giả sử (*) đúng với \(n=k\). Tức là : \(1^3+2^3+3^3+....+k^3=\left(1+2+...+k\right)^2\).
Ta cần chứng minh \(n=k+1\) cũng đúng với (*). Thật vậy , ta có :
\(1^3+2^3+3^3+.....+\left(k+1\right)^3\)
\(=1^3+2^3+....+k^3+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+\left(k+1\right)^3\)
Xét biểu thức \(\left(k+1\right)^2+2.\left(k+1\right).\left(1+2+3+....+k\right)\)
\(=\left(k+1\right)^2+2.\left(k+1\right)\cdot\frac{\left(k+1\right).k}{2}\)
\(=\left(k+1\right)^2+\left(k+1\right)^2.k=\left(k+1\right)^3\)
Do đó \(1^3+2^3+....+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+2.\left(k+1\right)\left(1+2+....+k\right)+\left(k+1\right)^2\)
\(=\left(1+2+3+....+k+k+1\right)^2\)
Vậy (*) đúng với \(n=k+1\) (3)
Từ (1) (2) và (3) suy ra \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) với mọi \(n\in N\).
13 tháng 7 2023
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
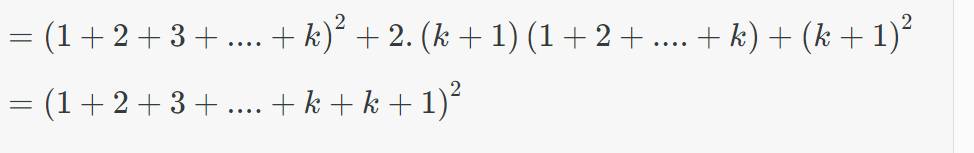
=>ĐPCM
5 tháng 1 2020
a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\)với m là 1 số nguyên dương
Biến đổi phương trình ta có :
\(\left(2n-1;2n+1\right)=1\)nên dẫn đến :
TH1 : \(2n-1=3u^2;2n+1=v^2\)
TH2 : \(2n-1=u^2;2n+1=3v^2\)
TH1 :
\(\Rightarrow v^2-3u^2=2\)
\(\Rightarrow v^2\equiv2\left(mod3\right)\)( vô lí )
Còn lại TH2 cho ta \(2n-1\)là số chính phương
b) Ta có :
\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)
\(\Leftrightarrow n^2=3k^2+3k+1\)
\(\Leftrightarrow4n^2-1=12k^2+12k+3\)
\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)
- Xét 2 trường hợp :
TH1 : \(\hept{\begin{cases}2n-1=3p^2\\2n+1=q^2\end{cases}}\)
TH2 : \(\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)
+) TH1 :
Hệ \(PT\Leftrightarrow q^2=3p^2+2\equiv2\left(mod3\right)\)( loại, vì số chính phương chia 3 dư 0 hoặc 1 )
+) TH2 :
Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\)( đpcm )
22 tháng 9 2015
Bài 1 :
Nếu n lẻ thì n + 1 chẵn do đó tổng n số tự nhiên liên tiếp là \(\frac{n.\left(n+1\right)}{2}\) là số chẵn nên không chia hết cho n vì n là số lẻ
Bài 2 :
Nếu n chẵn thì n + 1 lẻ do đó tổng n số tự nhiên liên tiếp là \(\frac{n.\left(n+1\right)}{2}\) là số chẵn nên chia hết cho n vì n là số chẵn
NN
1
AH
Akai Haruma
Giáo viên
15 tháng 2 2021
Lời giải:Gọi tổng bình phương của 5 số tự nhiên liên tiếp là:
$T=a^2+(a+1)^2+(a+2)^2+(a+3)^2+(a+4)^2$
$T=5a^2+20a+30=5(a^2+4a+6)=5[(a+2)^2+2]$
Vì $(a+2)^2$ là scp nên chia 5 dư $0,1,4$. Do đó $(a+2)^2+2$ chia $5$ dư $1,2,3$
$\Rightarrow T$ chia hết cho $5$ nhưng không chia hết cho $25$ nên $T$ không phải là scp.
Ta có đpcm.