Cho hinh thang ABCD(AB//CD),O là giao điểm 2 đường chéo AC và BD
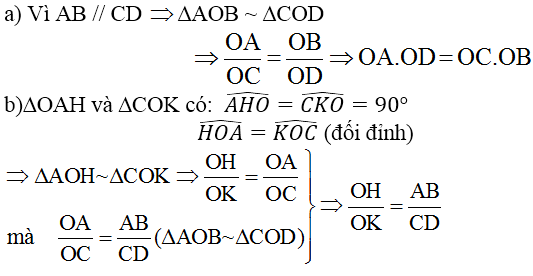
a) chứng minh rằng OA.OD=OB.OC
b)đường thẳng O vuông góc với AB và CD theo thứ tự H và K
chứng minh rằng OH/OK=AB/CD
c) tìm trên đường chéo BD điểm M sao cho đường thẳng qua M // với AB bị 2 cạnh AD,BC và hai đường chéo AC và BD chia thành 3 phần bằng nhau

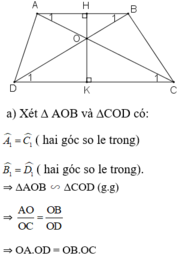
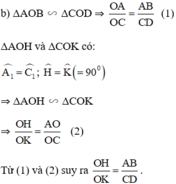


a, Xét 2 tam giác : AOB và COD
\(\widehat{A_1}=\widehat{C_1}\)( 2 góc so le trong )
\(\widehat{B_1}=\widehat{D_1}\)( 2 góc so le trong )
\(\Rightarrow\Delta AOB~\Delta COD\left(gg\right)\)
\(\Rightarrow\frac{AO}{OC}=\frac{OB}{OD}\)
\(\Rightarrow AO.OD=OC.OB\)
b, \(\Delta AOB~\Delta COD\Rightarrow\frac{OA}{OC}=\frac{AB}{CD}\left(1\right)\)
\(\Delta AOH\)và \(\Delta COK\)có :
\(\Rightarrow\frac{OH}{OK}=\frac{AO}{OC}\left(2\right)\)
Từ (1)(2) => \(\frac{OH}{OK}=\frac{AB}{CD}\)