Chứng minh rằng nếu 1 hình thẳng có hai và chỉ có hai trục đối xứng thì hai trục đối xứng đó phải vuông góc với nhau?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tứ giác có hai trục đối xứng cắt nhau thì các cặp cạnh đối bằng nhau (tính chất các đoạn thẳng đối xứng với nhau qua một đường thẳng). Vậy nó là hình bình hành (1)
Do các cặp cạnh đối song song với nhau mà lại đối xứng với nhau nên các cặp cạnh đối phải song song với trục đối xứng. Hai trục đối xứng vuông góc với nhau nên hai cạnh kề nhau phải vuông góc với nhau (2)
Từ (1) và (2) ta suy ra tứ giác đó là hình chữ nhât (theo định nghĩa)

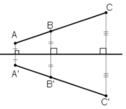
b) Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.
c) Đúng. Tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.
d) Sai.
Mọi đoạn thẳng AB đều có hai trục đối xứng là đường thẳng AB và đường trung trực của đoạn thẳng AB.
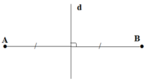

Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng

a)
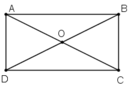
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
b)

Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.
Vậy ta có điều phải chứng minh.

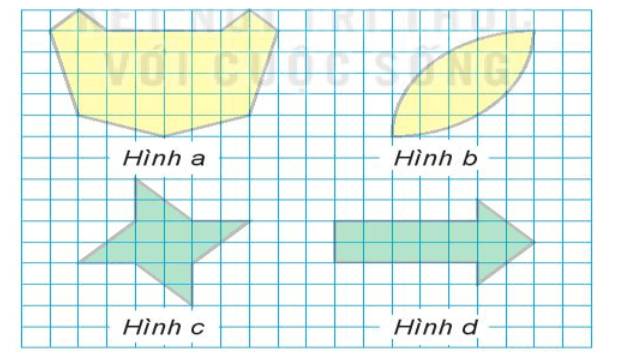
a) Hình không có trục đối xứng: hình c
b) Hình chỉ có một trục đối xứng: hình d, hình a
c) Hình có hai trục đối xứng: hình b
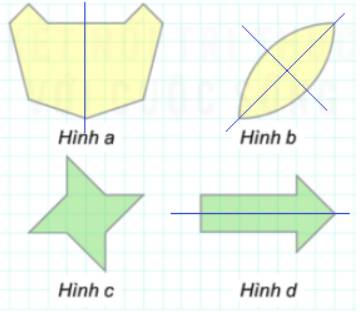
a) Hình c) không có trục đối xứng.
b) Hình a) và hình d) có đúng một trục đối xứng
c) Hình b) có hai trục đối xứng.

* Hình vuông có 4 trục đối xứng gồm 2 đường chéo của hình vuông và 2 đường thẳng đi qua trung điểm từng của cặp cạnh đối diện của hình vuông
* Hinh tròn có vô số trục đối xứng là các đường thẳng đi qua tâm của hình vuông.




HBH MJJM VJF UIJKNH ,MVNJF JMFJ HYIJ454 BN JV