một công ty vận tải điều một số xe tải đến kho hàng để chở 21 tấn hàng. khi đến kho hàng thì có 1 xe bị hỏng nên để hở hết lượng hàng đó, mỗi xe phải chở thêm 0,5 tấn so với dự định ban đầu. hỏi lúc đầu công ty đã điều đến kho hàng bao nhiêu xe. biết rằng khối lượng hàng chở ở mỗi xe là như nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (xe) là số xe mà công ty đã điều đến ban đầu (x>1).
Theo dự định, mỗi xe chở 21/x tấn hàng.
21/x tấn hàng của xe bị hỏng chia đều cho x-1 xe còn lại, mỗi xe được 0,5 tấn, ta có phương trình:
21/x:(x-1)=0,5 \(\Rightarrow\) \(\left\{{}\begin{matrix}x=7\left(nhận\right)\\x=-6\left(loại\right)\end{matrix}\right.\).
Vậy: ban đầu công ty đã điều đến kho hàng 7 xe.

Lời giải:
Giả sử số xe ban đầu dự định là $a$. ĐK: $a\in\mathbb{N}^*$.
Mỗi xe chở $\frac{90}{a}$ tấn hàng.
Theo bài ra ta có: 90=(a-2)(\frac{90}{a}+0,5)$
$\Leftrightarrow \frac{a}{2}-\frac{180}{a}-1=0$
$\Leftrightarrow a^2-2a-360=0$
$\Leftrightarrow (a-20)(a+18)=0$
Vì $a$ là số tự nhiên nên $a=20$

Gọi số xe đã điều khiển đến kho hàng lúc đầu là :x(xe,x thuộc u,x>1)
Nên số xe thực tế cho hàng là :x-1 xe;
Dự định mỗi xe chở 21/x tấn hàng
hàng
Thực tế mỗi xe phải chở thêm 0,5 tấn so với dự dih ban đầu nên :
21/x-1-21/x=0,5
Suy ra :x^2 - x -42 =0
<=>=7 (thỏa mãn x thuộc u ,x > 1) \(x_2\)= -6 loai
Vậy số xe lúc ban đầu là 7 xe

Gọi số xe lúc đầu là x (xe) (x > 1)
Số tấn hàng mỗi xe phải chở theo dự định là: $\frac{21}{x}$21x 21/xtấn
Thực tế có (x - 1) xe => Mỗi xe phải chở : $\frac{21}{x-1}$21x−1 21/x-1 tấn
Theo bài cho : Mỗi xe chở thêm so vơi dự định là 0,5 tấn nên ta có phương trình:
$\frac{21}{x-1}$21x−1 $\frac{21}{x}$21x 21/x-1=21/x + 0,5
=> 21x = 21(x - 1) + 0,5x.(x - 1)
<=> 0,5x2 - 0,5x - 21 = 0
<=> x2 - x - 42 = 0 <=> x2 - 7x + 6x - 42 = 0
<=> (x - 7).(x+6) = 0 <=> x = 7 hoặc x = - 6 (Loại)
Vậy có 7 xe lúc đầu

Gọi số xe lúc đầu là x (xe) (x > 1)
Số tấn hàng mỗi xe phải chở theo dự định là: \(\frac{21}{x}\) tấn
Thực tế có (x - 1) xe => Mỗi xe phải chở : \(\frac{21}{x-1}\) tấn
Theo bài cho : Mỗi xe chở thêm so vơi dự định là 0,5 tấn nên ta có phương trình:
\(\frac{21}{x-1}\)=\(\frac{21}{x}\) + 0.5
=> 21x = 21(x - 1) + 0,5x.(x - 1)
<=> 0,5x2 - 0,5x - 21 = 0
<=> x2 - x - 42 = 0 <=> x2 - 7x + 6x - 42 = 0
<=> (x - 7).(x+6) = 0 <=> x = 7 hoặc x = - 6 (Loại)
Vậy có 7 xe lúc đầu

Gọi số xe lúc đầu là x (xe) (x > 1)
Số tấn hàng mỗi xe phải chở theo dự định là: \(\frac{21}{x}\) tấn
Thực tế có (x - 1) xe => Mỗi xe phải chở : \(\frac{21}{x-1}\) tấn
Theo bài cho : Mỗi xe chở thêm so vơi dự định là 0,5 tấn nên ta có phương trình:
\(\frac{21}{x-1}\) = \(\frac{21}{x}\) + 0,5
=> 21x = 21(x - 1) + 0,5x.(x - 1)
<=> 0,5x2 - 0,5x - 21 = 0
<=> x2 - x - 42 = 0 <=> x2 - 7x + 6x - 42 = 0
<=> (x - 7).(x+6) = 0 <=> x = 7 hoặc x = - 6 (Loại)
Vậy có 7 xe lúc đầu

Gọi số xe ban đầu là x, x ∈ ℕ * (xe) nên số hàng theo kế hoạch mỗi xe chở là 24/x (tấn)
Số xe thực tế là x + 2 (xe) nên số hàng thực tế mỗi xe chở là 24/(x+2) (tấn)
Theo bài ra ta có phương trình:
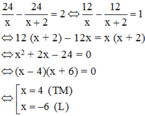
Vậy số xe ban đầu là 4 xe
Đáp án: A

Gọi số xe dự định ban đầu là x (x nguyên dương)
Số hàng mỗi xe dự định phải chở: \(\frac{21}{x}\) (tấn)
Số hàng mỗi xe thực tế phải chở: \(\frac{21}{x-1}\)
Theo bài ra ta có pt:
\(\frac{21}{x-1}-\frac{21}{x}=\frac{1}{2}\)
\(\Leftrightarrow x\left(x-1\right)=42x-42\left(x-1\right)\)
\(\Leftrightarrow x^2-x-42=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-6\left(l\right)\end{matrix}\right.\)
Gọi x(xe) là số xe ban đầu(Điều kiện: \(x\in Z^+\))
Ban đầu mỗi xe phải chở là: \(\dfrac{21}{x}\)(tấn)
Theo đề, ta có phương trình: \(\dfrac{21}{x-1}-\dfrac{1}{2}=\dfrac{21}{x}\)
\(\Leftrightarrow\dfrac{42x}{2x\left(x-1\right)}-\dfrac{x\left(x-1\right)}{2x\left(x-1\right)}=\dfrac{42\left(x-1\right)}{2x\left(x-1\right)}\)
Suy ra: \(42x-x^2+x=42x-42\)
\(\Leftrightarrow-x^2+41x-42x+42=0\)
\(\Leftrightarrow x^2-x-42=0\)
\(\Leftrightarrow x^2-7x+6x-42=0\)
\(\Leftrightarrow x\left(x-7\right)+6\left(x-7\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-7=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-6\left(loại\right)\end{matrix}\right.\)
Vậy: Lúc đầu có 7 xe