Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
a/ Ta có góc BDC=90 độ ( góc nt chăn nửa đường tròn)
suy ra góc ADH = 90 độ ( kề bù )
góc BEC= 90 độ ( góc nt chắn nửa đường tròn)
suy ra góc AEH = 90 độ ( kề bù )
Tư giác ADHE có góc ADH + góc AEH = 90 độ + 90 độ = 180 độ
Hại góc ở vị tri đối nhau . Do đó tứ giác ADHE nt đường tròn.
b/
c/Ta có góc BDC = 90 độ ( góc nt chắn nửa đt)
góc BEC = 90 độ ( góc nt chắn 1/2 đt)
Tứ giác BDEC có hai đỉnh kề D và E cùng nhìn BC dưới một góc vuông . Do đó tứ giác BDEC nt
suy ra góc BDE + góc BCE = 180 độ (1)
Mặt khác : góc ADE + góc BDE = 180 độ ( kề bù ) (2)
(1) (2) suy ra góc ADE = góc ACB
Xét tam giác ADE và tam giác ACB có
goc BAC chung
goc ADE = góc BAC (cmt)
suy ra tam giác ADE đồng dạng tam giác ACB (g.g)
nên AD/AC = AE/AB
hay AD.AB =AE.AC.
a) góc CEB là góc nội tiếp chắn nửa đường tròn
=> góc CEB =90 độ => góc BEA=90 độ (kb)
tam giác AEB có góc A=45 độ => tam giác AEB vuông cân =E
=> AE=EB
b) góc BDC là góc nội tiếp chắn nửa đường tròn
=> góc BDC=90 độ => góc HDA=90 độ (kb) (1)
góc BEA=90 độ => góc HEA=90 độ (2)
từ (1),(2) => góc HDA + góc HEA=180 độ
=> tứ giác DAEH nội tiếp
=)))
a: góc BDC=góc BEC=90 độ
=>CD vuông góc AB, BE vuông góc AC
góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
a: Xét ΔAEB vuông tại E và ΔADC vuông tại D có
góc EAB chung
Do đó:ΔAEB\(\sim\)ΔADC
Suy ra: AE/AD=AB/AC
hay AE/AB=AD/AC
Xét ΔAED và ΔABC có
AE/AB=AD/AC
góc EAD chung
Do đó: ΔAED\(\sim\)ΔABC
Suy ra: AE/AB=ED/BC
hay \(AE\cdot BC=ED\cdot AB\)
b: Xét ΔBDC vuông tại D và ΔBFA vuông tại F có
góc FBA chung
Do đó: ΔBDC\(\sim\)ΔBFA
Suy ra: BD/BF=BC/BA
hay \(BD\cdot BA=BF\cdot BC\)
Xét ΔCEB vuông tại E và ΔCFA vuông tại F có
góc FCA chung
Do đó: ΔCEB\(\sim\)ΔCFA
Suy ra CE/CF=CB/CA
hay \(CE\cdot CA=CB\cdot CF\)
\(BD\cdot BA+CE\cdot CA=BF\cdot BC+CF\cdot BC=BC^2\)
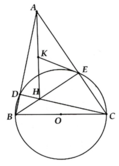
a/ Do tam giác ABE vuông có góc A=45o ==> tam giác ABE vuông cân ==> AE=BE
b/ Tứ giác ADHE có góc D +góc E= 90o+90o =180o
==> ADHE nội tiếp
c/Gọi I là trung điểm của AH ==> IA=IF ==> góc IAF=góc IFA (1)
Có O là trung điểm của BC ==> OF=OB ==> góc OFB=góc OBF (2)
Mà góc OBF= góc IAF ( cùng phụ góc ACB) (3)
(1), (2), (3) ==> góc IFA= góc OFB
==> góc AEB = góc IEO
==> góc IEO= 90o
==> đpcm