Cho đoạn thẳng AB và trung điểm O của đoạn thẳng đó. Trên 2 nửa mặt phẳng đối nhau bờ AB, kẻ hai tia Ax, By sao cho góc BAx=góc ABy, rồi lấy trên Ax hai điểm C và E (E nằm giữa A và C), trên By hai điểm D và F (F nằm giữa B và D) sao cho AC=BD,AE=BFChứng minha,OC=OD, OE=OFb,Ba điểm C,O,D thẳng hàng, ba điểm E,O,F thẳng hàngc,ED=CFMÌNH ĐANG CẦN GẤP,GIẢI CỤ THỂ GIÚP MÌNH...
Đọc tiếp
Cho đoạn thẳng AB và trung điểm O của đoạn thẳng đó. Trên 2 nửa mặt phẳng đối nhau bờ AB, kẻ hai tia Ax, By sao cho góc BAx=góc ABy, rồi lấy trên Ax hai điểm C và E (E nằm giữa A và C), trên By hai điểm D và F (F nằm giữa B và D) sao cho AC=BD,AE=BF
Chứng minh
a,OC=OD, OE=OF
b,Ba điểm C,O,D thẳng hàng, ba điểm E,O,F thẳng hàng
c,ED=CF
MÌNH ĐANG CẦN GẤP,GIẢI CỤ THỂ GIÚP MÌNH NHA
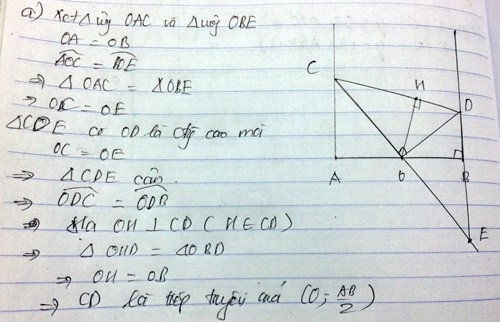
(để chứng minh OC =OD ta xét tam giác)
Xét tam giác OCA và tam giác ODB
AC=BD(gt)
góc CAO bằng góc DOB ( gt vì Góc BAx=ABy)
AO=BO ( O là trung điểm của AB)
Vậy tam giác OCA= tam giác ODB (c.g.c)
=> OC= OD ( 2 cạnh tương ứng)
Chứng MInh tương tự => OE=OF
b)để cm C,O,D thẳng hàng theo kiến thức lớp 7 nên CM 3 điểm tạo thành 1 góc bằng 180 độ. CM góc COD bằng 180 độ
Ta có ^COA+^COB= 180 độ
DOB + COB = COD
Mà ^COA = ^DOB ( 2 góc tương ứng của tam giác vừa CM ở í a)
=> DOB +COB bằng 180 độ
=>COD bằng 180
Vậy C, O, D thẳng hàng
CMTT( chứng minh tương tự )=> E, O,F thằng hàng
c)cái này cũng xét tam giác mà, chả khó j đâu
Cho mình xin cái :)
Bài làm
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)