GIÚP MÌNH VỚI !
Một con thuyền với vận tốc 2 km/h vượt qua một khúc sông nước chảy mạnh mất 5 phút. Biết rằng đương đi của con thuyền tạo với bờ một góc 600 . Tính chiều rộng của khúc sông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.35.
Áp dụng định lý Pitago:
$AH^2=AB^2-BH^2=AC^2-CH^2$
$\Rightarrow 2AH^2=AB^2+AC^2-(BH^2+CH^2)$
$=BC^2-(BH^2+CH^2)=(BH+CH)^2-(BH^2+CH^2)$
$=2BH.CH$
$\Rightarrow AH^2=BH.CH=2.64=128$ (cm)
$\Rightarrow AH=8\sqrt{2}$ (cm)
$\tan B=\frac{AH}{BH}=4\sqrt{2}$
$\Rightarrow \widehat{B}=79,98^0$
$\tan C=\frac{AH}{CH}=\frac{\sqrt{2}}{6}$
$\Rightarrow \widehat{C}=10,02^0$

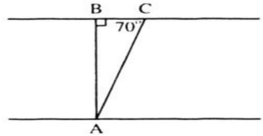
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
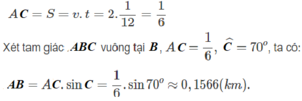
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.

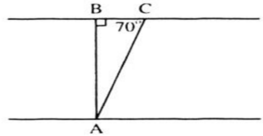
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
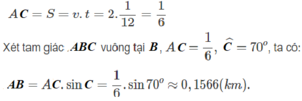
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.

Gọi AB là đoạn đường mà con thuyền đi được trong 6p, BH là chiều rộng của khúc sông
=>ΔBHA vuông tại H
AB=20*1/10=2(km)=2000(m)
Xét ΔBHA vuông tại H có BH=BA*sinA
=>\(BH=2000\cdot sin40\simeq1285,58\left(m\right)\)