Ai giải bài này giùm mình đi ngày mai mình thi rồi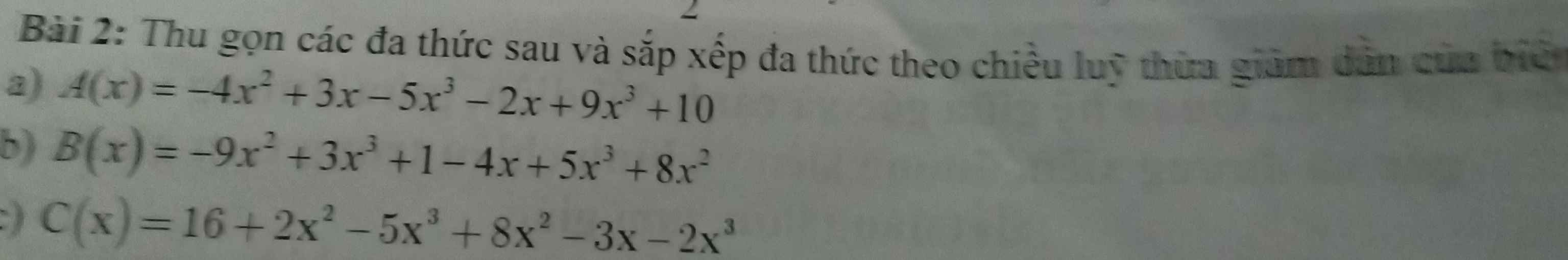
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔKMB vuông tại B và ΔKNA vuông tại A có
KM=KN
góc K chung
DO đó: ΔKMB=ΔKNA
b: Ta có: ΔKMB=ΔKNA
nên MB=NA
c: Xét ΔANM vuông tại A và ΔBMN vuông tại B có
MN chung
AN=BM
Do đó: ΔANM=ΔBMN

a: Xét ΔADB và ΔADC có
AD chung
DB=DC
AB=AC
Do đó: ΔADB=ΔADC
b: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác
c: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)
Do đó: ΔAED=ΔAFD
Suy ra: DE=DF

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

nếu bạn sd áy tính casio thì vào mode, 7(table) sau đó nhập biểu thức nhấn = ; -5 =; 5 =;1=; tùy theo yêu cầu của đề tìm số lớn hay nhỏ nhất thì chọn

\(=\dfrac{x^4+4x^2-3x^2-12+2x+1}{x^2+4}\)
\(=x^2-3+\dfrac{2x+1}{x^2+4}\)

a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt



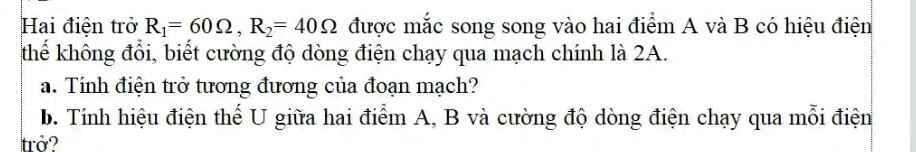
\(A\left(x\right)=4x^3-4x^2+x+10\)
\(B\left(x\right)=8x^3-x^2-4x+1\)
\(C\left(x\right)=-7x^3+10x^2-3x+16\)