
mọi người giúp em 2 bài này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a độ tụ của thấu kính là:
D=\(\dfrac{1}{f}=\dfrac{1}{-0,3}=\dfrac{-10}{3}\)
b. áp dụng công thức thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{d'}=\dfrac{1}{f}-\dfrac{1}{d}=\dfrac{1}{-30}-\dfrac{1}{20}=\dfrac{-1}{12}\Rightarrow d'=-12\)
tính chất của ảnh: là ảnh ảo ngược chiều
số phóng đại: k=\(\dfrac{-d'}{d}=\dfrac{-\left(-12\right)}{20}=\dfrac{3}{5}\)
độ cao của ảnh: A'B'=kAB<->A'B'=\(\dfrac{3}{5}\cdot5=3\)

Câu 10:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)
\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)
\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)
b: \(A=\dfrac{x+2}{x+1}\)
=>A không phụ thuộc vào biến y
Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)
Câu 12:
a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)
\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)
b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)
\(x+\dfrac{1}{3}=\dfrac{10}{3}\)
=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)
=>\(x=\dfrac{9}{3}=3\left(loại\right)\)
Vậy: Khi x=3 thì A không có giá trị
c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x^2-4x+5}\)
\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x-2=0
=>x=2

3) \(\sqrt{\left(x-2\right)\left(x+1\right)}\) thì (x-2)(x+1)>0
=> x2 -x-2>0
=> x2 - x - \(\dfrac{1}{2}\)- \(\dfrac{3}{2}\)>0
= (x+\(\dfrac{1}{4}\))2 - 3/2 >0
=> x+ 1/4>3/2
=> x>5/4
4) Có x đâu mà tìm bạn??

Câu 6:
Gọi kim loại đó là \(R\)
\(\rightarrow Oxit:R_2O_3\)
Giả sử dd \(H_2SO_4\) phản ứng \(a\left(mol\right)\)
\(PTHH:R_2O_3+3H_2SO_4\rightarrow R_2\left(SO_4\right)_3+3H_2O\)
\(\left(mol\right)\) \(\dfrac{a}{3}\) \(a\) \(\dfrac{a}{3}\)
\(m_{ddH_2SO_4}=\dfrac{98a.100}{10}=980a\left(g\right)\)
\(C\%_{ddspu}=12,9\left(\%\right)\Leftrightarrow\dfrac{\left(2R+288\right).\dfrac{a}{3}}{\left(2R+48\right).\dfrac{a}{3}+980a}.100=12,9\\ \Leftrightarrow\dfrac{\dfrac{\left(2R+288\right)}{3}}{\dfrac{\left(2R+48\right)}{3}+980}.100=12,9\\ \Leftrightarrow R=56\left(Fe\right)\\ \rightarrow Oxit:Fe_2O_3\)
Câu 7:
\(a.n_{NaOH}=\dfrac{60.10\%}{40}=0,15\left(mol\right)\)
Đặt \(C\%_{HCl}=a\left(\%\right)\Rightarrow n_{HCl}=\dfrac{40a}{100.36,5}=\dfrac{4a}{365}\left(mol\right)\)
\(C\%_{NaCl}=5,85\%\Leftrightarrow\dfrac{m_{NaCl}}{60+40}.100=5,85\Leftrightarrow m_{NaCl}=5,85\left(g\right)\Leftrightarrow n_{NaCl}=0,1\left(mol\right)\)
\(PTHH:NaOH+HCl\rightarrow NaCl+H_2O\)
(mol) 0,1 0,1 0,1
Lúc này ta có: \(n_{HCl}=\dfrac{4a}{365}=0,1\Leftrightarrow a=9,125\left(\%\right)\)
Câu b làm tương tự!!!

vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
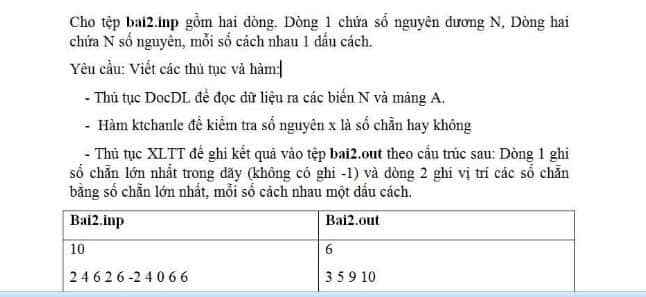
Bài 2:
#include <bits/stdc++.h>
using namespace std;
long long n,i,a[1000],x;
int main()
{
freopen("bai2.inp","r",stdin);
freopen("bai2.out","w",stdout);
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
for (i=1; i<=n; i++)
if (a[i]%2==0)
{
x=a[i];
break;
}
cout<<x<<endl;
for (i=1; i<=n; i++)
if (a[i]==x) cout<<i<<" ";
return 0;
}