Tìm số dư khi chia B=21+23+25+27+...+22015+22017 chia cho 21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=(1+2+2^2)+2^3(1+2+2^2)+...+2^2013(1+2+2^2)+2^2016
=7(1+2^3+...+2^2013)+2^2016
Vì 2^2016 chia 7 dư 1
nên A chia 7 dư 1


Nếu bớt số càn tìm đi đúng bằng số dư khi chia số đó cho 23 thì được số mới chia hết cho 23
Sô mới là
23x21=483
Khi chia số mới cho 92 ta được thương là 5 và dư 23
Hiệu số dư của hai phép chia khi chia số cần tìm và số mới cho 92 là
30‐23=7
Số cần tìm là
483+7=490

Gọi thương của phép chia a:21 là x, a:27 là y (x,y thuộc N*)
Ta có: 21.x+3=27.y+12
<=> 21x=27y+9
<=> 7x=9y+3=3(3y+1)
=> \(x=\frac{3\left(3y+1\right)}{7}\)
Mà x thuộc N* => 3y+1 phải chia hết cho 7 => 3y+1=(1,7)
+/ 3y+1=1 => y=0 (Loại)
+/ 3y+1=7 => y=2 (Nhận)
=> x=3
Số cần tìm là: a=3.21+3=66
Đáp số: a=66

Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2

\(S=2+2.2^2+3.2^3+...+2016.2^{2016}\)
\(2S=2^2+2.2^3+3.2^4+...+2016.2^{2017}\)
\(2S-S=S=\text{}\text{}\text{}\text{}2^2+2.2^3+3.2^4+...+2016.2^{2017}-2-2.2^2-3.2^3-...-2016.2^{2016}\)
\(S=2\left(0-1\right)+2^2\left(1-2\right)+2^3\left(2-3\right)+...+2^{2016}\left(2015-2016\right)+2^{2017}.2016\)
\(S=-\left(2+2^2+2^3+...+2^{2016}\right)+2^{2017}.2016\)
\(\)Đặt \(A=2+2^2+2^3+...+2^{2016}\)
\(2A=2^2+2^3+2^4+...+2^{2017}\)
\(2A-A=A=2^2+2^3+2^4+...+2^{2017}-2-2^2-2^3-...-2^{2016}\)
\(A=2^{2017}-2\)
Thay vào S ta được:
\(S=-2^{2017}+2+2^{2017}.2016\)
\(S=2^{2017}.2015+2\)
Ta có \(S+2013=2^{2017}.2015+2+2013\)
\(S+2013=2^{2017}.2015+2015\)
\(S+2013=2015\left(2^{2017}+1\right)\)
Suy ra \(S+2013⋮2^{2017}+1\)
Vậy \(S+2013⋮2^{2017}+1\) (đpcm)

Ta có A=20+21+22+23+...2100
2A=21+22+...+2101
2A-A=(21+22+...+2100)-(20+21+...+2100)
A=2101-1
Mà 2101-1=(........02)-1=........01 chia 100 dư 1
Chúc bạn học tốt.
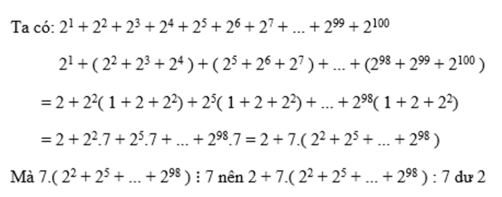
B = 21 + 23 + 25 + ......+22015 + 22017
4B = 22 . ( 21 + 23 + 25 +.....+ 22015 + 22017 )
4B = 23 + 25 + 27 + 2 9 + ...... + 22019
4B - B = 22019 - 21
=> 3B = 22019 - 21
=> B = \(\frac{2^{2019}-2^1}{3}\)