Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có AECF là hình bình hành=> EF cắt AC ở trung điểm I của mỗi đường
AMCN là hình bình hành=>MN cắt AC ở trung điểm của mỗi đường
=>EF cắt MN ở trung điểm mỗi đường=> ĐPCM
.a.
Vì `EF` là đường trung trực MB.
=> `EM=EB`
=> `ΔEMB` cân tại E
=> \(\widehat{EMB}=\widehat{EBM}\)
Chứng minh tương tự được: \(\widehat{FMB}=\widehat{FBM}\)
Vì `AM=DN` mà AM//DN
=> Tứ giác `AMND` là hình bình hành.
b.
Từ câu (a) suy ra:
ME//BF
BE//FM
=> Hình bình hành MEBF có `EF⊥MB`
=> Tứ giác MEBF là hình thoi
a) *) Chứng minh AMNB là hình bình hành:
Do O là giao điểm của AC và BD
Mà ABCD là hình bình hành (gt)
⇒ O là trung điểm của AC và BD
Do MN // AB (gt)
⇒ OM // CD
∆ACD có
O là trung điểm AC
OM // CD
⇒ M là trung điểm AD
⇒ AM = AD : 2 (1)
Do MN // AB (gt)
⇒ ON // AB
∆ABC có:
O là trung điểm AC (cmt)
ON // AB (cmt)
⇒ N là trung điểm BC
⇒ BN = BC : 2 (2)
Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ AM // BN
Từ (1) và (2) ⇒ AM = BN
Tứ giác AMNB có:
AM // BN (cmt)
AM = BN (cmt)
⇒ AMNB là hình bình hành
*) Chứng minh APCQ là hình bình hành
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AP // CQ
Tứ giác APCQ có:
AP // CQ (cmt)
AP = CQ (gt)
⇒ APCQ là hình bình hành
c) Do O là trung điểm AC (cmt)
M là trung điểm AD (cmt)
⇒ OM là đường trung bình của ∆ACD
⇒ OM = CD : 2 (3)
Do O là trung điểm AC (cmt)
N là trung điểm BC (cmt)
⇒ ON là đường trung bình của ∆ABC
⇒ ON = AB : 2
Mà AB = CD (do ABCD là hình bình hành)
⇒ OM = ON
⇒ O là trung điểm MN
Do APCQ là hình bình hành (cmt)
O là trung điểm AC (cmt)
⇒ O là trung điểm PQ
Tứ giác MPNQ có:
O là trung điểm MN (cmt)
O là trung điểm PQ (cmt)
⇒ MPNQ là hình bình hành
⇒ MP // NQ và MQ = NP
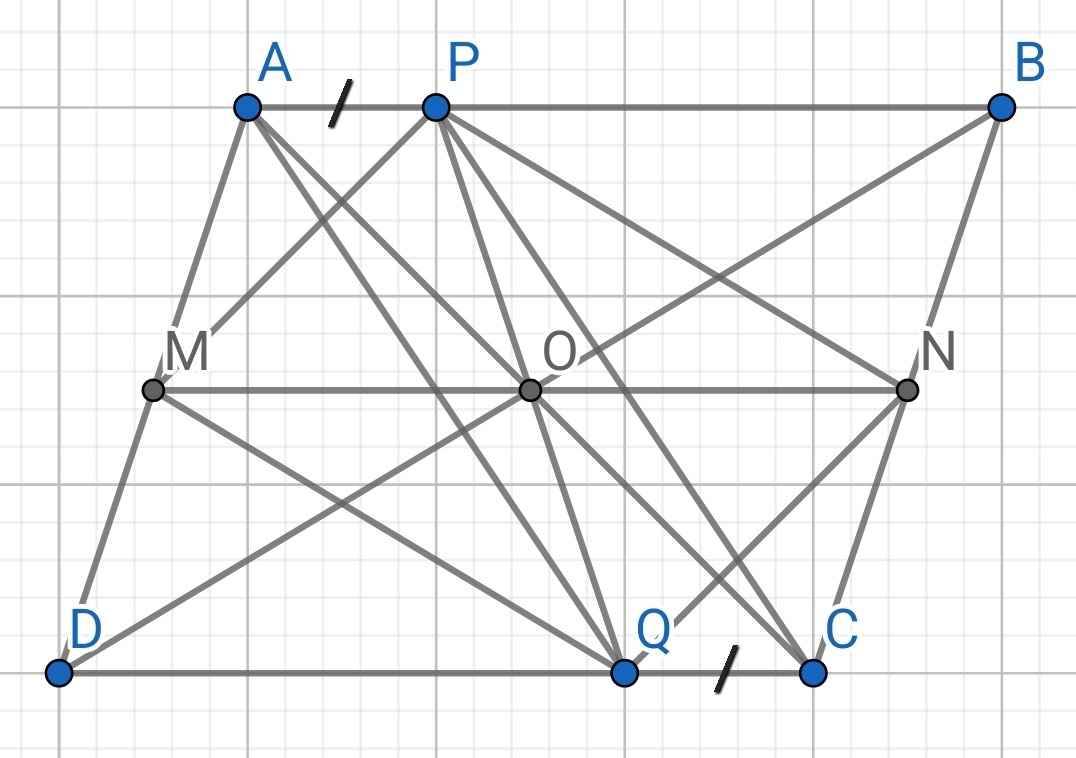
a. Do AE = CF nên ED = BF.
Xét tam giác MBF và NDE có:
BM = DN (gt)
BF = DE (cmt)
\(\widehat{MBF}=\widehat{NDE}\) (Hai góc đối của hình bình hành)
\(\Rightarrow\Delta MBF=\Delta NDE\left(c-g-c\right)\Rightarrow MF=EN.\)
Tương tự EM = NF. Từ đó suy ra EMFN là hình bình hành.
b. Dễ thấy MBND là hình bình hành. Xét đường chéo của hình bình hành:
Trong hbh ABCD: AC cắt BD tại trung điểm mỗi đường
Trong hbh MBND: BD cắt MN tại trung điểm mỗi đường
Trong hbh EMFN: MN cắt EF tại trung điểm mỗi đường
Vậy 4 đường thẳng trên đồng quy tại O.