cho tam giác ABC cân AB=AC=10cm ; BC=16cm, đường cao AH , gọi I thuộc AH , AI =1/3 AH . Vẽ Cx // AH ,Cx giao BI tại D .
a) Tính các góc của tam giác ABC .
b) Tính diện tích của tam giác ABC
Ai giải giúp mk với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 7 2017
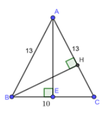
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
Mặt khác:
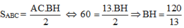
Xét ABH vuông tại H có:
Đáp án cần chọn là: A
4 tháng 3 2022
a: Xét ΔACB có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
Suy ra: \(\widehat{BCA}=\widehat{DCA}\)
hay CA là tia phân giác của góc BCD
c: Xét ΔCDB có CD=CB
nên ΔCDB cân tại C
CM
23 tháng 2 2018
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 6cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 102 - 62 = 64 ⇒ AM = 8m. Chọn C
T
1
31 tháng 8 2017
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)
11 tháng 1 2022
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
10 tháng 2 2018
Lời giải:
Tam giác ABC cân tại A nên đường phân giác AH đồng thời là đường trung trực của BC
Áp dụng định lý pitago ta được:
\(AH^2=AB^2-BH^2=10^2-6^264\Rightarrow AH=8\)
Áp dụng tính chất đường phân giác ta được:
18 tháng 1 2022
a: AB+BC>AC>AB-BC
=>15>AC>5
=>AC=10(cm)
=>ΔABC cân tại A
b: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM
16 tháng 2 2022
https://hoc24.vn/cau-hoi/.4762222558882
-Bạn chỉ cần thay đổi một chút thôi.
đề sai rồi bn câu b hình như là tinh Sabcd chứ