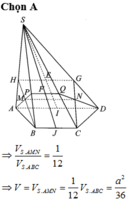
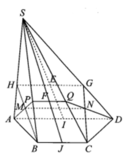
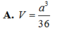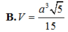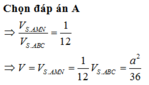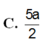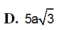Cho hình chóp S.ABC, đáy ABC là tam giác vuông tại B, BC = a, cạnh bên SA vuông góc với đáy và SA = a. Gọi MN là đoạn vuông góc chung của hai đường thẳng SC và AB, \(\left(M\in SC,N\in AB\right)\). Tỷ số \(\dfrac{AN}{AB}\) bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Lấy điểm D sao cho ABCD là hình chữ nhật

Tam giác SAD vuông cân tại A, E là trung điểm SD nên
![]()

Chọn D
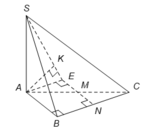
Xác định được
![]()
![]()
Gọi N là trung điểm BC, suy ra MN//AB.
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó
![]()
![]()
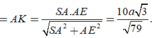

Đáp án B
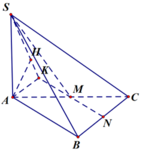
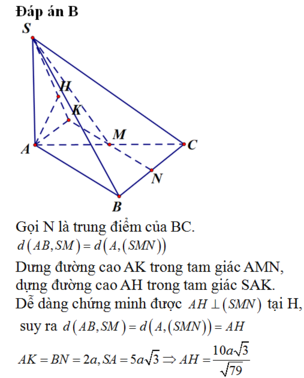
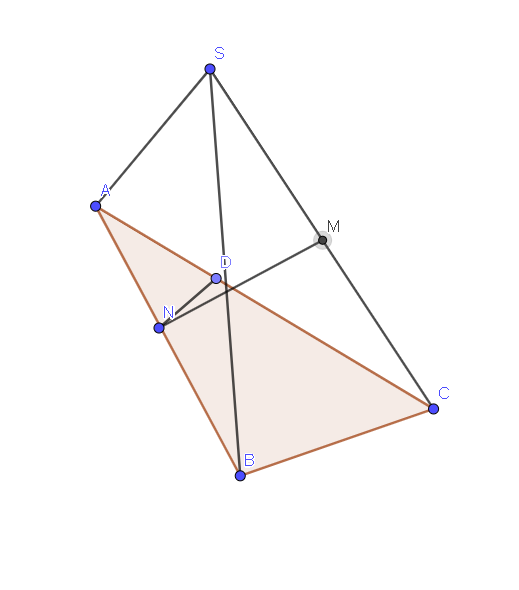
Gọi N là trung điểm của BC.
d A B , S M = d A , S M N
Dưng đường cao AK trong tam giác AMN, dựng đường cao AH trong tam giác SAK.
Dễ dàng chứng minh được A H ⊥ S M N tại H, suy ra d A B , S M = d A , S M N = A H
A K = B N = 2 a , S A = 5 a 3 ⇒ A H = 10 a 3 79

Gọi N là trung điểm của BC, dựng hình bình hành ABNP.
Ta có:
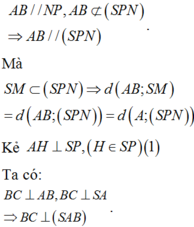
Mà
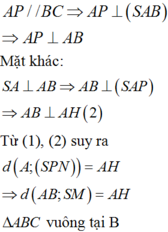
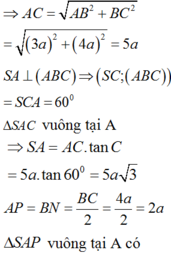
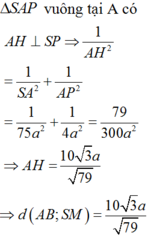
Chọn: B

Đáp án B
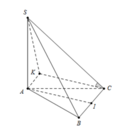
Dựng hình bình hành AKCI khi đó S C ; A I ⏜ = S C ; C K ⏜
Ta có: A B = C K = A B 2 + B C 2 2 = a 6 2
S K = S A 2 + A K 2 = S A 2 + C I 2 = a 6 2
Khi đó cos S C K ⏜ = S C 2 + C K 2 − S K 2 2 S C . C K = 2 3 > 0 Do đó c os S C ; A I ⏜ = 2 3