cho △ABC nt (O:R). các tiếp tuyến tại B và C cắt nhau tại N, H là trực tâm tam giác BCN, qua A kẻ đg thẳng song song vs BC cắt đg tròn tại M, đg thẳng MN cắt cung BC tại K.
a, tg OBNC nội tiếp.
b, NB.MB =BK.MN và BO=BH
giúp mk vs mk cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MB,MC là tiếp tuyến
=>MB=MC
mà OB=OC
nên OM là trung trực của BC
Xét ΔMEB và ΔMBF có
góc MBE=góc MFB
góc EMB chung
=>ΔMEB đồng dạng với ΔMBF
=>MB^2=ME*MF=MH*MO

Lời giải:
*** Mình chưa thấy điểm $I$ có vai trò gì trong bài này.
Gọi $D$ là giao điểm $BC, AN$ và $L$ là giao $AN$ với $(O)$
Dễ thấy $\triangle ABN=\triangle MCN$ do:
$AB=MC$ (tính chất cung bị chặn bởi 2 dây song song)
$NB=NC$
$\widehat{ABN}=\frac{1}{2}\text{sđc(AB>)}=\frac{1}{2}\text{sđc(MC>)}=\widehat{MCN}$
Do đó:
$\widehat{BAD}=\widehat{BAN}=\widehat{CMN}=\widehat{CAH}$
$\Rightarrow \widehat{BAH}=\widehat{CAD}$
Ta có:
$\frac{HB}{CH}=\frac{S_{ABH}}{S_{ACH}}=\frac{AB.AH.\sin BAH}{AC.AH.\sin CAH}=\frac{AB.\sin BAH}{AC\sin CAH}$
$=\frac{AB}{AC}.\frac{\sin BAH}{\sin CAH}=\frac{AB}{AC}.\frac{\sin CAD}{\sin BAD}=\frac{AB}{AC}.\frac{\sin CAL}{\sin BAL}=\frac{AB}{AC}.\frac{\sin CBL}{\sin BCL}=\frac{AB}{AC}.\frac{LC}{BL}(*)$
Mà:
Dễ cm $\triangle ABN\sim \triangle BLN, \triangle ACN\sim \triangle CLN$
$\Rightarrow \frac{AB}{BL}=\frac{BN}{LN}=\frac{CN}{LN}=\frac{AC}{CL}$
$\Rightarrow \frac{LC}{BL}=\frac{AC}{AB}(**)$
Từ $(*); (**)\Rightarrow \frac{BH}{HC}=\frac{AB}{AC}.\frac{AC}{AB}=1$
$\Rightarrow BH=HC$ nên $H$ là trung điểm của $BC$

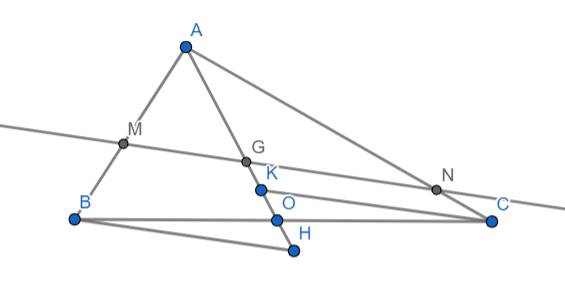
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)

Ta có : góc AMO = góc ANO = 900 (t/c tiếp tuyến)
Mặt khác I là tđ BC => OI vuông góc BC (t/c đường kính và dây) => góc AIO = 900
=> 5 điểm A, M, O, I, N cùng nằm trên một đường tròn
Ta có góc MAI = góc MNI (AMIN nt), mà góc EBI = góc MAI (đồng vị, do AM // BE) => góc MNI = góc EBI hay góc ENI = góc EBI
=> Tứ giác NBEI nội tiếp => góc BNE = góc BIE. Mà góc BNE = góc BCM (cùng chắn cung MB trong (O))
=> góc BIE = góc BCM => IE // CM
(bài này lớp 9 mà)
a)
có góc OBN = góc OCN = 90 độ
lại ở vị trí đối nhau nên tứ giác OBNC nội tiếp
b)
ta có góc BMK = góc KBN ( 2 góc nội tiếp chắn cung BK)
xét tam giác NBK và tam giác NMB có
góc N chung
góc NBK = góc BMN ( cmt)
=> tam giác NBK ∼ tam giác NMB
=> \(\dfrac{NB}{BK}=\dfrac{MN}{MB}\)
=> NB.MB=BK.MN
ta có OC vuông góc với NC
BH vuông góc với NC ( H là trực tâm)
=> OC // BH (1)
lại có OB vuông góc với BN
CH vuông góc với BN ( H trực tâm )
=> OB // CH (2)
từ (1) và (2) => OBHC là hình bình hành
lại có OB = OC ( 2 bán kính )
=> OBHC là hình thoi
=> OB = BH ( đpcm )