Cho hai đường tròn tâm O bán kính R và (O') bsn kính R/2,tiếp xúc ngoại tại A .trên (O)l ấy điểm B sao cho AB = R và điểm M trên cung lớn AB.Tia MA cắtđường tròn (O’) tại điểm thứ hai là N.Qua N kẻ dường thẳng song song với AB cắt đường thẳng MB tại Q và cắt đường tròn (O’) tại P.CM a) tam giác AOM động dạng tam giác O'AM b) độ dài NQ ko phụ thuộc vào M .cứu với mong vẽ cả hình nữa ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).

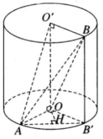
Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2

a, HS tự làm
b, HS tự làm
c, Chú ý hình thang vuông OEFO’ và xét đường trung bình của hình thang này
d, Từ I kẻ đường thảng song song với EF cắt OE tại M , cắt O’F tại N
Đặt BH=2R; CH= 2R’
∆IOM vuông tại M có:
I M 2 = I O 2 - O M 2 = R + r 2 - R - r 2 = 4 R r
Tương tự , ∆ION có I N 2 = 4 R ' r
Suy ra IM+IN=EF=AH
Vậy 2 R r + 2 R ' r = 2 R R '
=> r R + R ' = R R '
=> r = R R ' R + R ' 2
a: ΔAOM cân tại O
=>góc OAM=góc OMA
ΔAO'N cân tại O' nên góc O'AN=góc O'NA
mà góc OAM=góc O'AN
nên ΔOAM đồng dạng với ΔO'AN
b: MA/NA=OA/O'A
=>MA/(NA+MA)=MA/MN=OA/(OA+O'A)=2/3
AB//NQ
=>AB/NQ=MA.MN
=>R/NQ=2/3
=>NQ=3R/2 ko đổi