giải ra nữa ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2}{x}=\dfrac{x}{x+1}\left(ĐKXĐ:x\ne0;x\ne-1\right)\)
\(\Leftrightarrow\dfrac{2\left(x+1\right)}{x\left(x+1\right)}=\dfrac{x^2}{x\left(x+1\right)}\)
\(\Rightarrow x^2=2x+2\)
\(\Leftrightarrow x^2-2x-2=0\)
\(\Leftrightarrow x^2-2x+1-3=0\)
\(\Leftrightarrow\left(x-1\right)^2-3=0\)
\(\Leftrightarrow\left(x-1-\sqrt{3}\right)\left(x-1+\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1-\sqrt{3}=0\\x-1+\sqrt{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{3}\left(nhận\right)\\x=1-\sqrt{3}\left(nhận\right)\end{matrix}\right.\)
-Vậy \(S=\left\{1+\sqrt{3};1-\sqrt{3}\right\}\)



a)\({\dfrac{3}{4}}\)số rác dễ phân hủy là
\({\dfrac{3}{4}}\).12=9(kg)
An nhận đc số cây sen đá là:
9:3=3(cây)
b) đội An thu đc số kg rác khó phân hủy là:
9:\({\dfrac{3}{20}}\)=60(kg)
Đ/s: a,3 cây
b,60 kg

a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC
hay DECB là hình thang


1 city => cities (trên tg có nhiều thành phố)
2 A => traditionally (trạng từ bổ nghĩa cho động từ)
3 B => contribute (thì hiện tại đơn, chủ ngữ số nhiều dúng Vnguyen)
4 D => her first boyage (tàu thuyền du lịch chuyển sang sở hữu dùng her)
5 C => richest (đằng trước so sánh nhất nên đằng sau cũng dùng so sánh nhất)

7 D(How often:Bao lâu-dùng để chỉ tần suất)
8 C(newreaders:người đọc tin tức)
9 A(remote control:điều khiển)
10 B(so:vì vậy)

Có sai đâu nhỉ?
Dòng 2 từ trên xuống hình thứ nhất bạn nhân module \(3i\) vào 2 vế, khi đó vế phải là 12, còn vế trái:
\(\left|3i.iz_2-3i.1+3i.2i\right|=\left|-3iz_2-3i-6\right|=\left|\left(-3iz_2\right)-6-3i\right|\)
Dòng 2 từ dưới đếm lên hình 2:
\(I_1\left(-6;-10\right)\) ; \(I_2\left(6;3\right)\Rightarrow\overrightarrow{I_1I_2}=\left(12;13\right)\Rightarrow I_1I_2=\sqrt{12^2+13^2}\)
Một công thức tính độ dài vecto rất cơ bản




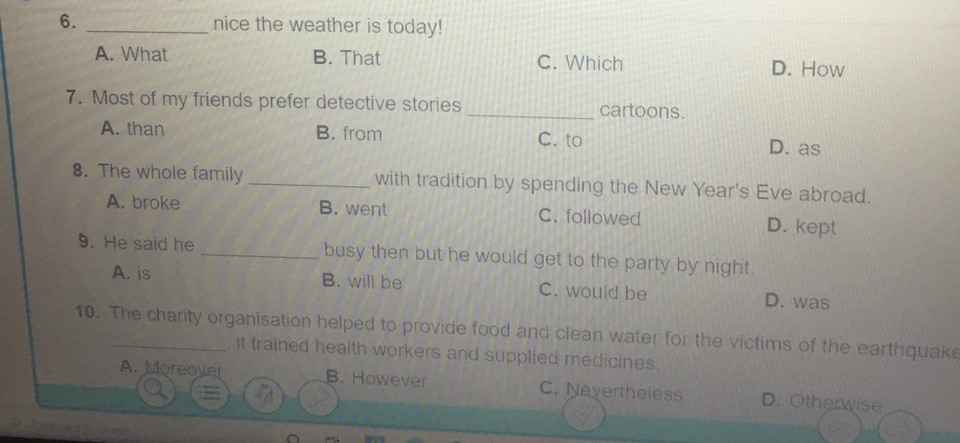

 cho thêm giải thích nữa ạ
cho thêm giải thích nữa ạ

\(a,\)Đặt \(f\left(x\right)=0\)
\(\Rightarrow2x^2+5,2=0\)
\(\Rightarrow2x^2=-5,2\)
\(\Rightarrow x^2=-10,4\)
\(\Rightarrow x=\sqrt{-10,4}\left(ktm\right)\)
Vậy \(f\left(x\right)=\varnothing\)