Vẽ tam giác ABC cân tại A. Có Bc=6cm , AB=5cm
Gọi M là trung điểm của BC
a) CMR : AM vuông góc BC
b) CMR : AM là phân giác góc BAC
c) CMR : AM là trung trực của B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM vừa là đường phân giác vừa là đường cao
b: Xét ΔABC có
AM là đường trung tuyến
AO=2/3AM
Do đó: O là trọng tâm của ΔABC
=>BO là đường trung tuyến ứng với cạnh AC
hay E là trung điểm của AC
c: Ta có: O là trọng tâm của ΔABC
mà CO cắt BA tại F
nên F là trung điểm của AB
Xét ΔABE và ΔACF có
AB=AC
\(\widehat{BAE}\) chung
AE=AF
Do đó: ΔABE=ΔACF
Suy ra: BE=CF
1 tháng 2 2019
tu ve hinh :
a; b, xet tamgiac AMF va tamgiac AME co : AM chung
goc AFM = goc AEM = 90 do MF | AC va ME | AB (gt)
goc FAM = goc EAM do AM la phan giac cua goc BAC (gt)
=> tamgiac AMF = tamgiac AME (ch - gn)
=> AE = AF (dn) (1)
AB = AC do tamgiac ABC can tai A (gt)
AE + EB = AB
AF + FC = AC
=> EB = FC
xet tamgiac BEM va tamgiac CFM co : goc B = goc C do tamgiac ABC can tai A (gt)
goc MEB = goc MFC do ...
=> tamgiac BEM = tamgiac CFM (cgv - gnk)
=> MB = MC
c, (1) => tamgiac AEF can tai E (dn)
=> goc AEF = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc B = (180 - goc BAC) : 2
=> goc AEF = goc B ma 2 goc nay dong vi
=> EF // BC (dh)
KN
1 tháng 2 2019
Giải
Bạn tự vẽ hình
a; b, Xét \(\Delta AMF\) va \(\Delta AME\) có : AM chung
\(\widehat{AFM}=\widehat{AEM}=90^0\) do MF\(\perp\)AC va ME\(\perp\)AB
\(\widehat{FAM}=\widehat{EAM}\)do AM la phân giác của \(\widehat{BAC}\)
\(\Rightarrow\Delta AFM=\Delta AME\)
\(\Rightarrow AE=AF\) (1)
AB = AC do \(\Delta ABC\) cân tại A
AE + EB = AB
AF + FC = AC
\(\Rightarrow\) EB = FC
Xét \(\Delta BEM\) và \(\Delta CFM\) có : \(\widehat{B}\) = \(\widehat{C}\) do \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{MEB}=\widehat{MFC}\)
\(\Rightarrow\Delta BEM=\Delta CFM\)
\(\Rightarrow\) MB = MC
c, Từ (1) suy ra \(\Delta AEF\)cân tại E
\(\Rightarrow\widehat{AEF}=\left(180-\widehat{BAC}\right)\div2\)
\(\Delta ABC\) cân tại A \(\Rightarrow\)\(\widehat{B}\)= (180 - \(\widehat{BAC}\)) : 2
\(\Rightarrow\widehat{AEF}=\widehat{B}\) mà hai góc này đồng vị
\(\Rightarrow EF//BC\)
2 tháng 12 2018
a, Xét tam giác AMB và tam giác AMC có
AB = AC (gt)
AM chung
MB = MC ( M là trung điểm BC )
=> tam giác AMB = tam giác AMC (c.c.c)
=>\(\widehat{BAM}=\widehat{CAM}\)
=> AM là phân giác góc BAC
b, Vì tam giác AMB = tam giác AMC (cmt)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)
Ta có : \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{AMB}+\widehat{AMB}=180^o\)
\(\Rightarrow\widehat{AMB}=90^o\)
\(\Rightarrow AM\perp BC\left(ĐPCM\right)\)
M
2 tháng 12 2018
a) Xét tam giác ABC có : AB = AC
=> Tam giác ABC cân tại A
Mà AM là đường trung tuyến ứng với BC ( vì M là trung điểm của BC)
=>AM vừa là đường trung tuyến đồng thời là đường phân giác
Do đó : AM là tia phân giác của góc BAC(đpcm)
b)Vì tam giác ABC cần tại A ( theo câu a )
Nên đường phân giác AM đồng thời là đường cao
=> AM vuông góc với BC ( đpcm )
7 tháng 11 2015
Xét tam giác AMB và tam giác AMC có:
AB=AC(giả thiết)
AM chung
MB=MC(M là trung điểm BC)
Từ 3 điều trên, ta có tam giác AMB=tam giác AMC=>góc B=góc C
b/ Ta có tam giác AMB=tam giác AMC=>góc BAM=góc CAM=>AM là tia phân giác của góc BAC
c/ Ta có tam giác AMB=tam giác AMC=>góc AMB=góc AMC mà tổng 2 góc này bằng 180 độ=>góc AMB=góc AMC=>AM vuông góc với BC
14 tháng 1 2022
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
14 tháng 1 2022
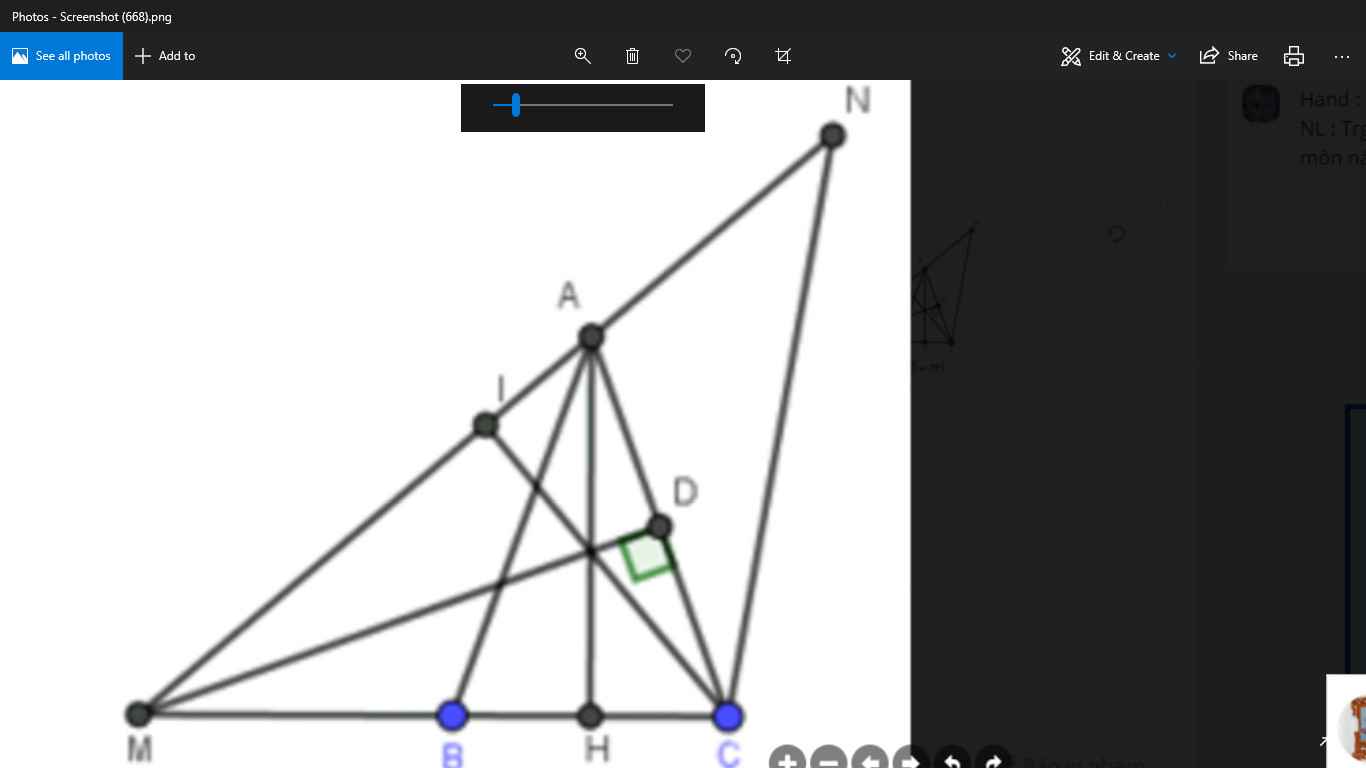
\(\text{a)}\Delta ABC\text{ cân tại }A\text{ có }\widehat{A}=40^0\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
\(\text{Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(BH=CH\text{(H là trung điểm BC)}\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{ÂHB}=\widehat{AHC}\)
\(\text{mà }\widehat{AHB}+\widehat{AHC}=180^0\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow AH\perp BC\)
\(\text{b)}\Delta AMC\text{ cân tại M}\text{ vì MD là đường trung trực}\)
\(\Rightarrow\widehat{MAD}=\widehat{MCD}=70^0\)
\(\text{Ta có:}\widehat{MAD}=\widehat{MAH}+\widehat{CAH}\)
\(\Rightarrow\widehat{MAH}=\widehat{MAD}-\widehat{CAH}=70^0-\dfrac{40^0}{2}=50^0\text{(vì AH là phân giác }\widehat{BAC}\text{)}\)
\(\text{c)Xét }\Delta ABM\text{ và }\Delta CAN\text{ có:}\)
\(BM=AN\text{(cách lấy điểm N)}\)
\(AB=AC\left(cmt\right)\)
\(\widehat{ABM}=\widehat{CAN}=180^0-70^0=110^0\)
\(\Rightarrow\Delta ABM=\Delta CAN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\text{(hai cạnh tương ứng)}\)
\(\text{d)Xét }\Delta MIC\text{ và }\Delta NIC\text{ có:}\)
\(IC\text{ cạnh chung}\)
\(\widehat{MIC}=\widehat{NIC}=90^0\)
\(\widehat{IMC}=\widehat{INC}\text{(vì }\Delta ABM=\Delta CAN\text{)}\)
\(\Rightarrow\Delta MIC=\Delta NIC\left(gn.cgv\right)\)
\(\Rightarrow MI=NI\)
\(\Rightarrow\text{I là trung điểm MN}\)
a) Xét ΔAMB và ΔAMC ta có:
AB=AC ( tích chất tam giác cân)
AM=MC (giả thiết)
AM cạnh chung
⇒ ΔAMB = ΔAMC (c-c-c)
⇒ \(\widehat{AMB}=\widehat{AMC}\) (hai góc tương ứng), mà hai góc này kề bù nên
\(\widehat{AMB}=\widehat{AMC}=\dfrac{180}{2}=90^o\)
Vậy AM ⊥ BC (đpcm)
b) từ câu a ta có ΔAMB = ΔAMC nên:
\(\widehat{BAM}=\widehat{CAM}\) (hai góc tương ứng)
⇒ AM là tia phân giác của \(\widehat{BAC}\) (đpcm)
c) Ta có AM ⊥ BC (1)
BM=CM (2) vì AM vuông góc với BC và M cách đều BC (BM=CM)
từ (1) và (2) ⇒ AM là đường trung trực của AB
s ít thấy xu on hoc24 nhỉ?