Chứng minh rằng tâm của đường tròn đi qua 3 đỉnh của một tam giác vuông là trung điểm của cạnh huyền. Giúp mình nhanh với nha.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)

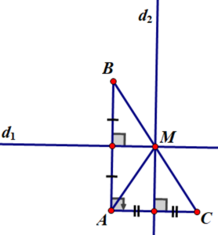
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
QUẢNG CÁO+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

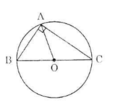
Hình a) + b)
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.
Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.
=> O là tâm của đường tròn đi qua A, B, C.
Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:
OA = OB = OC
Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)

a, Giả sử ∆ABC vuông tại A. Gọi O là trung điểm của BC
=> OA = OB = OC => O là tâm đường tròn đi qua A,B,C
b, Ta có OA = OB = OC => OA = 1 2 BC => ∆ABC vuông tại A

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền

- Lấy một điểm M bất kì trong không gian sao cho MA = MB = MC. Từ M kẻ MO vuông góc với mp(ABC). Các tam giác vuông MOA, MOB, MOC bằng nhau, cho ta OA = OB = OC.
- Suy ra O là tâm đường tròn ngoại tiếp tam giác ABC. Vậy các điểm M cách đều ba đỉnh của tam giác ABC nằm trên đường thẳng d đi qua tâm O của đường tròn ngoại tiếp tam giác ABC và vuông góc với mp(ABC). Ngược lại, lấy một điểm M' ∈ d, nối M'A, M'B, M'C.
- Do M'O chung và OA = OB = OC nên các tam giác vuông M'OA, M'OB, M'OC bằng nhau, cho ta M'A = M'B = M'C.
- Tức là điểm M' cách đều ba đỉnh A, B, C của tam giác ABC.
- Kết luận : Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là đường thẳng vuông góc với mp(ABC) và đi qua tâm của đường tròn ngoại tam giác ABC.
Vì tâm đường tròn đi qua 3 đỉnh của tam giác với mỗi tam giác chỉ có duy nhất 1 điểm.
Gọi I là trung điểm cạnh huyển BC của tam giác ABC vuông tại A.
Ta sẽ đi chứng minh I là tâm đường tròn đi qua 3 đỉnh tam giác ABC.
Thật vậy, trên tia đối tia IA , ta lấy điểm D sao cho IA=ID .
Vì I là trung điểm BC => IB=IC
Xét tam giác AIB và tam giác CID có:
AI=IC ; BI=ID ; AIB =CID (2 góc đối đỉnh)
=> Tam giác AIB =tam giác CID (c.g.c)
=> AB=CD; IAB = ICD
Vì IAB =ICD , mà 2 góc này ở vị trí so le trong
=> AB// CD Mà AB vuông góc với AC
=> CD vuông góc AC => ACD = 90
Xét tam giác BAC và DCA có:
AC chung ; AB=DC ; BAC = DCA =90
=> BAC = DCA(c.g.c)
=> BC = DA
Mà IB = IC = BC/2; AI=ID =DA/2
=> IB=IC=IA
=> I là tâm đường tròn đi qua A,B, C
A
B