Cho hình thang ABCD ( AB//CD; AB<CD). Gọi O là giao điểm hai đường chéo AC và BD.a. Cm: △OAB∼△OCDb. Đường thẳng đi qua O và song song với AB cắt AD, BC lần lượt tai H và K. Cm: O là trung điểm của HKc. Cm: HK/AB + HK/CD= 2Giúp mình với huhu sắp thi...
Đọc tiếp
Cho hình thang ABCD ( AB//CD; AB<CD). Gọi O là giao điểm hai đường chéo AC và BD.
a. Cm: △OAB∼△OCD
b. Đường thẳng đi qua O và song song với AB cắt AD, BC lần lượt tai H và K. Cm: O là trung điểm của HK
c. Cm: HK/AB + HK/CD= 2
Giúp mình với huhu sắp thi òi
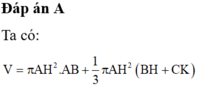
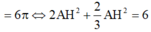
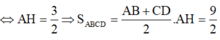
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔOAB\(\sim\)ΔOCD
b: Xét hình thang ABCD có HK//AB//CD
nên AH/AD=BK/BC(1)
Xét ΔADC có OH//DC
nên OH/DC=AH/AD(2)
Xét ΔBDC có OK//DC
nên OK/DC=BK/BC(3)
Từ (1), (2) và (3) suy ra OH=OK
hay O là trung điểm của HK