Tìm giá trị lớn nhất của hàm số f(x)=\(\frac{x}{x^2+2014x+1}\)(Với x>0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


f(x) = x3 +3/x = x3 + 1/x +1/x +1/x
cô si 4 số làm mất x là xong

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
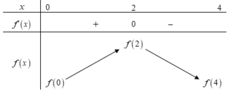
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)


\(f'\left(x\right)=\frac{\frac{\sqrt{x+1}}{\sqrt{x}}-\frac{\sqrt{x}}{\sqrt{x+1}}}{x+1}=\frac{1}{\sqrt{x}\left(\sqrt{x+1}\right)^3}>0;\forall x\in\left(0;4\right)\)
Mà f(x) liên tục trên [0;4] nên hàm số đồng biến trên [0;4]
\(\Rightarrow Maxf\left(x\right)_{\left[0;4\right]}=f\left(4\right)\)
YCBT \(\Leftrightarrow\begin{cases}m>1\\f\left(4\right)\le3\end{cases}\) \(\Leftrightarrow\begin{cases}m>1\\\frac{4+m}{\sqrt{5}}\le3\end{cases}\)\(\Leftrightarrow1< m< 3\sqrt{5}-4\)

\(F=\frac{x}{x^2+2}\)
với x > 0, áp dụng bđt Cauchy ta có :
\(x^2+2\ge2\sqrt{x^2+2}=2x\sqrt{2}\)
=> \(\frac{1}{x^2+2}\le\frac{1}{2x\sqrt{2}}\)
=> \(\frac{x}{x^2+2}\le\frac{1}{2\sqrt{2}}\)( x > 0 nên khi nhân vào cả hai vế bđt giữ chiều )
hay \(F\le\frac{1}{2\sqrt{2}}\)
đẳng thức xảy ra khi \(x=\sqrt{2}\)
vậy maxF = \(\frac{1}{2\sqrt{2}}\), đạt được khi \(x=\sqrt{2}\)

\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)

Chọn D
Ta có 3x.f(x) -
x
2
f
'
(
x
)
=
2
f
2
(
x
)
![]()
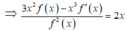
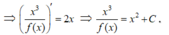
Thay x = 1 vào ta được 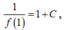 vì f(1) =
1
3
nên suy ra C = 2
vì f(1) =
1
3
nên suy ra C = 2
Nên  Ta có:
Ta có: 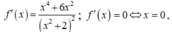
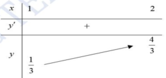
Khi đó, f(x) đồng biến trên [1;2]
Suy ra ![]()
Suy ra ![]()

tách x2+32 = (x2-4) +32
=) f(x) = (x+2)/4 + 9/(x-2) = [(x-2)/4 +9/(x-2)] + 1
cô si 2 số trong ngoặc vuông làm mất (X-2) là xong

Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
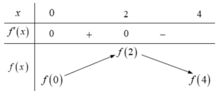
Từ bảng biến thiên ta có ![]()
Mặt khác ![]()
![]()
![]()
![]()
Suy ra ![]()

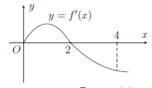
Ta có f(x) đạt giá trị lớn nhất khi \(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất.
Xét \(\frac{1}{f\left(x\right)}=\frac{x^2+2014x+1}{x}=x+\frac{1}{x}+2014\ge2\sqrt{x.\frac{1}{x}}+2014=2016\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x>0\\x=\frac{1}{x}\end{cases}}\Leftrightarrow x=1\)
\(Min\)\(\frac{1}{f\left(x\right)}=2016\Leftrightarrow x=1\)
Vậy \(Max\)\(f\left(x\right)=\frac{1}{2016}\Leftrightarrow x=1\)