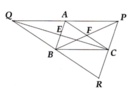
Cho tam giác ABC, trung tuyến CE và BF. Trên tia đối của tia FB lấy điểm P sao cho PF = FB, trên tia đối của tia EC lấy điểm Q sao cho QE = CE.
a, Chứng minh: AP = BC
b, Chứng minh: A là trung điểm của PQ
c, Chứng minh: BA + BC > 2BF
d, Gọi G là giao điểm của BP và QC. Chứng minh: QB, AG, PC đồng qui.
Mọi người giúp mình với ạ !

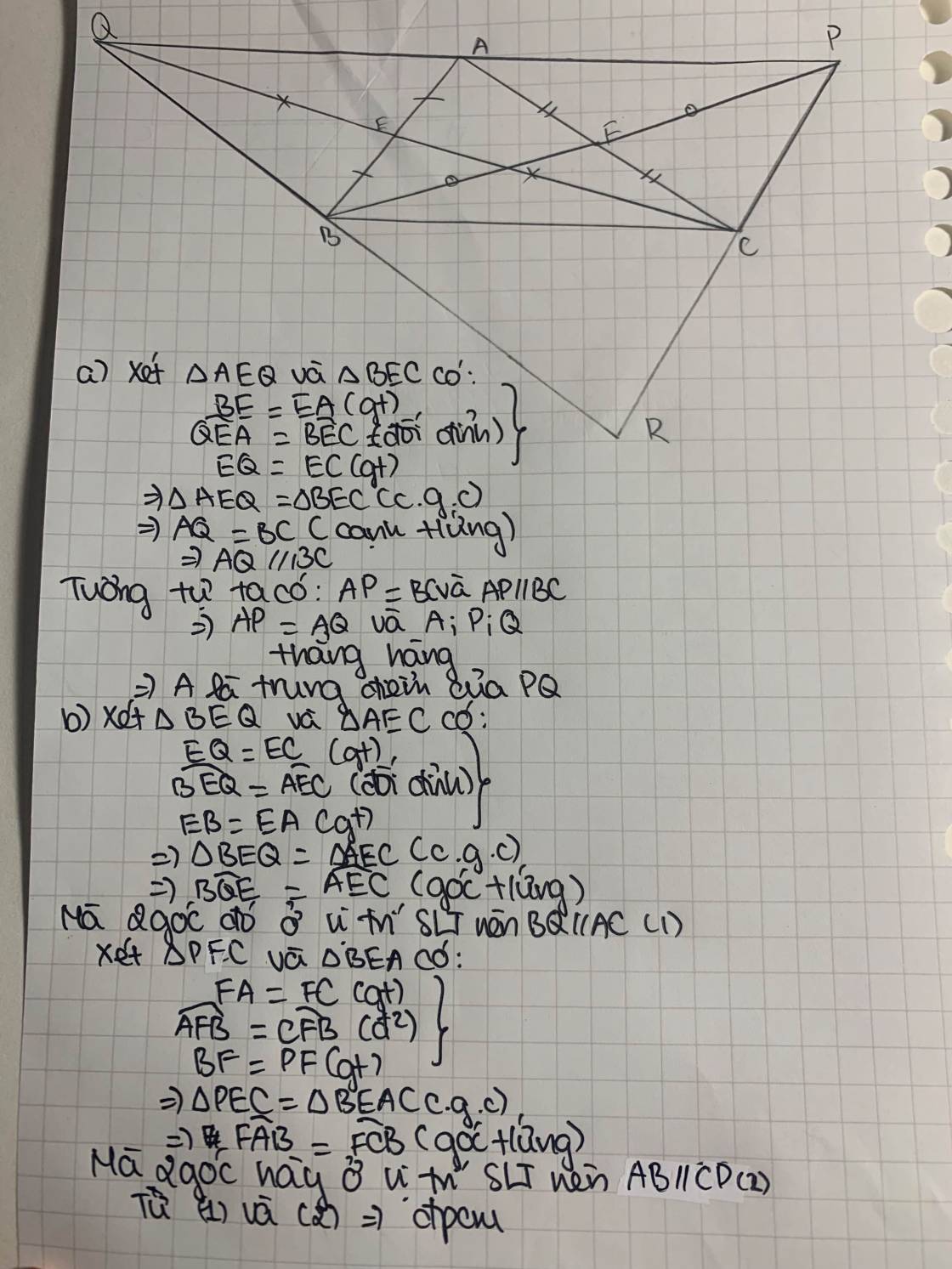


a: Xét tứ giác ABCP có
F là trung điểm chung của AC và BP
=>ABCP là hình bình hành
=>AP=BC và AP//BC
b: Xét tứ giác AQBC có
E là trung điểm chung của AB và QC
=>AQBC là hình bình hành
=>AQ//BC và AQ=BC
=>AP=AQ và AP//AQ
=>A là trung điểm của PQ
c: BA+BC=BC+CP>CP=2BF