
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



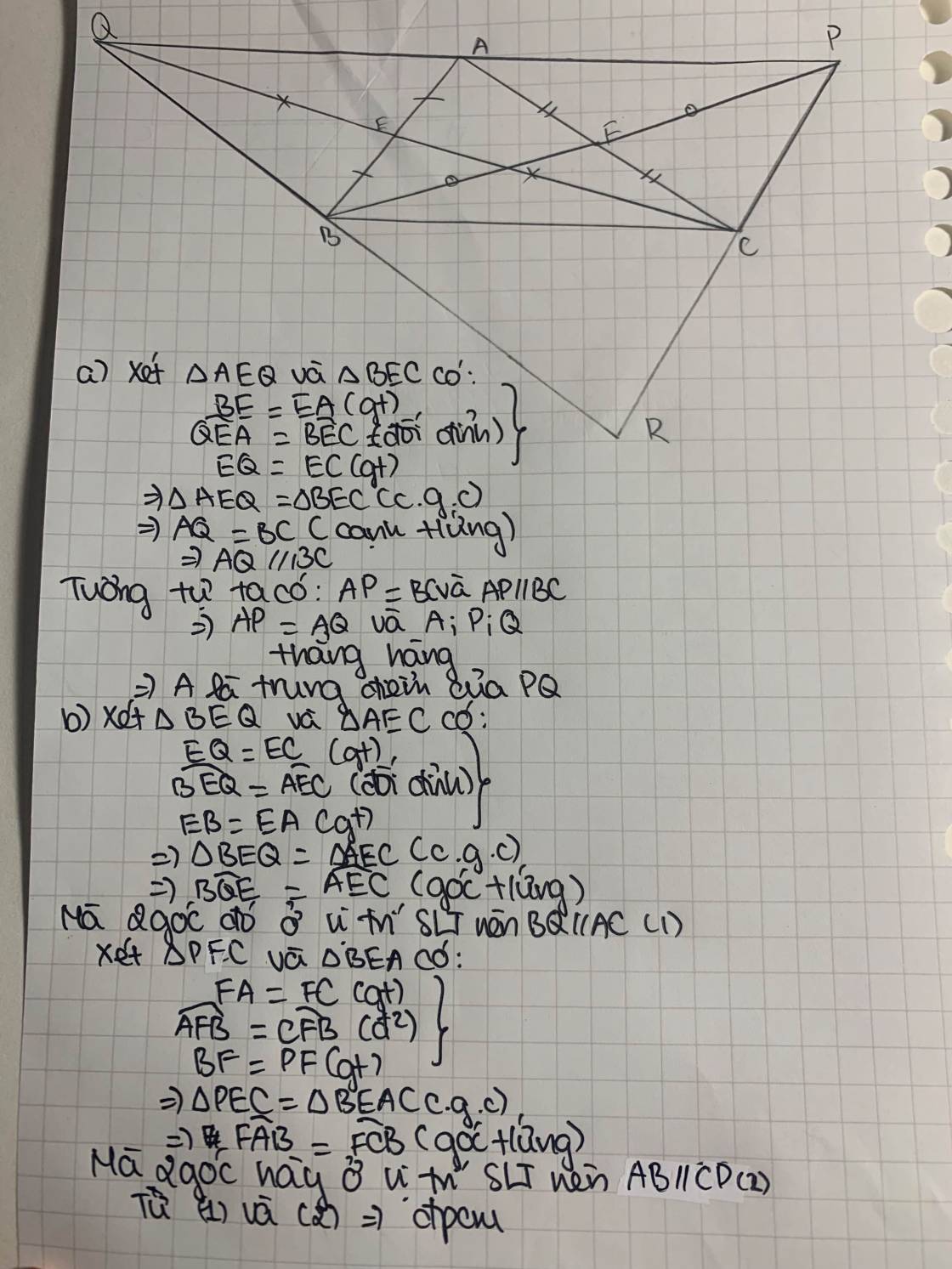
a) Xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=> tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.

a: Xét tứ giác ABCP có
F là trung điểm chung của AC và BP
nen ABCP là hình bình hành
Suy ra: AP//BC và AP=BC
Xét tứ giác AQBC có
E là trug điểm chung của AB và QC
nên AQBC là hình bình hành
Suy ra: AQ//BC và AQ=BC
=>AP=AQ
b: Ta có: AQ//BC
AP//BC
DO đó: P,A,Q thẳng hàng
c: Ta có: AQBC là hình bình hành
nên BQ//AC
Ta có: ABCP là hình bình hành
nên CP//AB

a) Xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=> tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ
c)
xét tam giác BEQ và tam giác AEC có
EQ=EC
BEQ=AEC đối đỉnh
EB=EA
=> tam giác BEQ = tam giác AEC(c.g.c)
=> BQE=AEC (góc tương ứng)
mà chúng ở vị trí so le trong nên BQ//AC.
xét tam giác PFC và BFA có:
FA=FC
AFB=CFP
BF=PF
=> tam giác PFC = BFA (c.g.c)
=> FAB = FCB(góc tương ứng)
mà chúng ở vị trí số le trong nên
CP//AB

a) Xét tam giác\(BAP\)có:
\(E,F\)lần lượt là trung điểm của \(BA,BP\)
nên \(EF\)là đường trung bình của tam giác \(BEF\).
Suy ra \(EF//AP,EF=\frac{1}{2}AP\).
Tương tự ta cũng có \(EF//AQ,EF=\frac{1}{2}AQ\).
Có qua \(A\)có \(AP,AQ\)đều song song với \(EF\)nên \(Q,A,P\)thẳng hàng.
mà \(AP=AQ\left(=2EF\right)\)suy ra \(A\)là trung điểm của \(PQ\).
b) Xét tam giác \(ABC\):
\(E,F\)lần lượt là trung điểm \(AB,AC\)
nên \(EF\)là đường trung bình của tam giác \(ABC\)
suy ra \(EF//BC,EF=\frac{1}{2}BC\).
suy ra \(BC//AQ,BC=AQ\)
do đó tứ giác \(ACBQ\)là hình bình hành.
suy ra \(BQ//AC\)
.Tương tự ta cũng chứng minh được \(ABCP\)là hình bình hành
suy ra \(CP//AB\).
c) \(BC=\frac{1}{2}PQ,BC//PQ\)nên \(BC\)là đường trung bình của tam giác \(PQR\).
Do đó \(B,C\)lần lượt là trung điểm của \(QR,PR\).
suy ra \(AC,AB\)là hai đường trung bình của tam giác \(PQR\)
suy ra \(AC=\frac{1}{2}QR,AB=\frac{1}{2}PR\).
\(P_{PQR}=PQ+QR+PR=2\left(AB+BC+CA\right)=2P_{ABC}\)
ta có đpcm.
d) Có \(RA,PB,QC\)là ba đường trung tuyến trong tam giác \(PQR\)do đó chúng đồng quy tại một điểm.
Ta có đpcm.
cam on ban nhieu lam :))))))))))))))))))))))))))))))))))))))))

xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=>. tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.
b) xét tam giác BEQ và tam giác AEC có
EQ=EC
BEQ=AEC đối đỉnh
EB=EA
=> tam giác BEQ = tam giác AEC(c.g.c)
=> BQE=AEC(góc tương ứng) mà chúng ở vị trí so le trong nên BQ//AC.
xét tam giác PFC và BFA có:
FA=FC
AFB=CFP
BF=PF
=. tam giác PFC = BFA (c.g.c)
=> FAB = FCB(góc tương ứng)
mà chúng ở vị trí so le trong nên
CP//AB
cho tớ 1 tick nhé! ^^ cảm ơn
vì Tam gáic AEQ = BEC nên QAE=CBE, mà chugns ở vị trí so le trong nên AQ//BC.
=> QAB=CBA
xét tam giác ABQ và tam giác ABC có
QAB=CAB
AB chung
CAB=QBA( AC//BQ)
vậy chúng bằng nhau(g.c.g)
AQB=ACB
mà AQB=CBR(đồng vị) từ hai điều này suy ra ACB=RBC
vì tam giác AFB=CFB nên A=C mà chúng ở vị trí so le trong nên AP//BC=>PAC=BCA
Xét tam giác ABC và PCA có
BAC=PCA(AB//PC)
AC chung
PAC=BCA(cmt)
vậy chúng bằng nhau theo truognừ hợp g.c.g
=>ABC=CPA
mà CPA=RCP( đồng vị) từ hai điều này suy ra ABC=RCB.
Xét tam giác ABC và RCB có
AQB=CBR
BC chung
CPA=RCP
vậy chúng bằng nhau theo truognừ hợp g.c.g
=> AB=RC;AC=RB(cạnh tuognư ứng)
* Vì AQ//BC,AP//BC, theo tiên đề Ơ-clit => ba điểm Q,A,P thẳng hàng
vì BC = AQ = AP nên BC = 1/2 QP
* Vì AC = BQ(cmt)
AC=BR(cmt)
nên AC = 1/2 QR
vì theo đề cho ba điểm Q,B,R đã thằng hàng nên không cần chứng minh. ba điểm P,C,R cũng vậy.
* Vì AB=CP(cmt)
AB=RC(cmt)
nên AB= 1/2 RP
ta có chu vi tam giác PQR = PQ + QR + RP = \(\frac{1}{2}BC+\frac{1}{2}AC+\frac{1}{2}AB=\frac{1}{2}\left(AB+AC+BC\right)=\frac{1}{2}\)chu vi ABC điều phải chứng minh.
d) Xét tam giác PQR có BQ=BR(cùng bằng AC)
CR=CP(cùng bằng AB)
AQ=AP(cmt) và Q,A,P thẳng hàng
suy ra B,C và A lần lượt là trung điểm của QR, RP và PQ.
gọi giao điểm của QC và BP là H
tam giác PQR có QC, PB và RA là các đuognừ trung tuyến giao nhau tại H nên H là trọng tâm. Xong
vậy 3 đường này đồng quy

a) xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=>. tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.
b) xét tam giác BEQ và tam giác AEC có
EQ=EC
BEQ=AEC đối đỉnh
EB=EA
=> tam giác BEQ = tam giác AEC(c.g.c)
=> BQE=AEC(góc tương ứng) mà chúng ở vị trí so le trong nên BQ//AC.
xét tam giác PFC và BFA có:
FA=FC
AFB=CFP
BF=PF
=. tam giác PFC = BFA (c.g.c)
=> FAB = FCB(góc tương ứng)
mà chúng ở vị trí so le trong nên
CP//AB
Có thể loại đường trung bình nữa à Tuân Huỳnh Ngọc Minh???!!!

a: Xét tứ giác ABCP có
F là trung điểm chung của AC và BP
nen ABCP là hình bình hành
Suy ra: AP//BC và AP=BC
Xét tứ giác AQBC có
E là trug điểm chung của AB và QC
nên AQBC là hình bình hành
Suy ra: AQ//BC và AQ=BC
=>AP=AQ
b: Ta có: AQ//BC
AP//BC
DO đó: P,A,Q thẳng hàng
c: Ta có: AQBC là hình bình hành
nên BQ//AC
Ta có: ABCP là hình bình hành
nên CP//AB

a: Xét tứ giác ABCP có
F là trung điểm chung của AC và BP
nen ABCP là hình bình hành
Suy ra: AP//BC và AP=BC
Xét tứ giác AQBC có
E là trug điểm chung của AB và QC
nên AQBC là hình bình hành
Suy ra: AQ//BC và AQ=BC
=>AP=AQ
b: Ta có: AQ//BC
AP//BC
DO đó: P,A,Q thẳng hàng
c: Ta có: AQBC là hình bình hành
nên BQ//AC
Ta có: ABCP là hình bình hành
nên CP//AB

a: Xét tứ giác ABCP có
F là trug điểm của AC
F là trung điểm của BP
Do đó: ABCP là hbh
=>AP//BC và AP=BC
Xét tứ giác AQBC có
E là trung điểm của AB
E là trung điểm của QC
Do đó: AQBC là hbh
=>AQ//BC và AQ=BC
=>AQ=AP
b: Ta có: AP//BC
AQ//BC
Do đó: P,A,Q thẳng hàng
c: Ta có: ABCP là hình bình hành
nên CP//AB