Question

[Ngô Ngọc Huyền]

Một xe tải có khối lượng M= 5tấn chuyển động đều khi đi lên cũng như đi xuống một cái dốc dài L= 2km. Lực kéo xe do động cơ sinh ra khi lên dốc là 2500N; khi xuống dốc là 500N. Cho rằng lực ma sát có giá trị không đổi khi xe lên và xuống dốc.

a) Tính độ cao của dốc.

b) Biết thời gian xe lên dốc lớn hơn 1,8phút so với thời gian xuống dốc. Tính vận tốc lên dốc và xuống dốc của xe nếu công suất động cơ sản ra khi lên dốc bằng 3,125 lần khi xuống dốc.

Answer 1

[nguyễn thị hương giang]

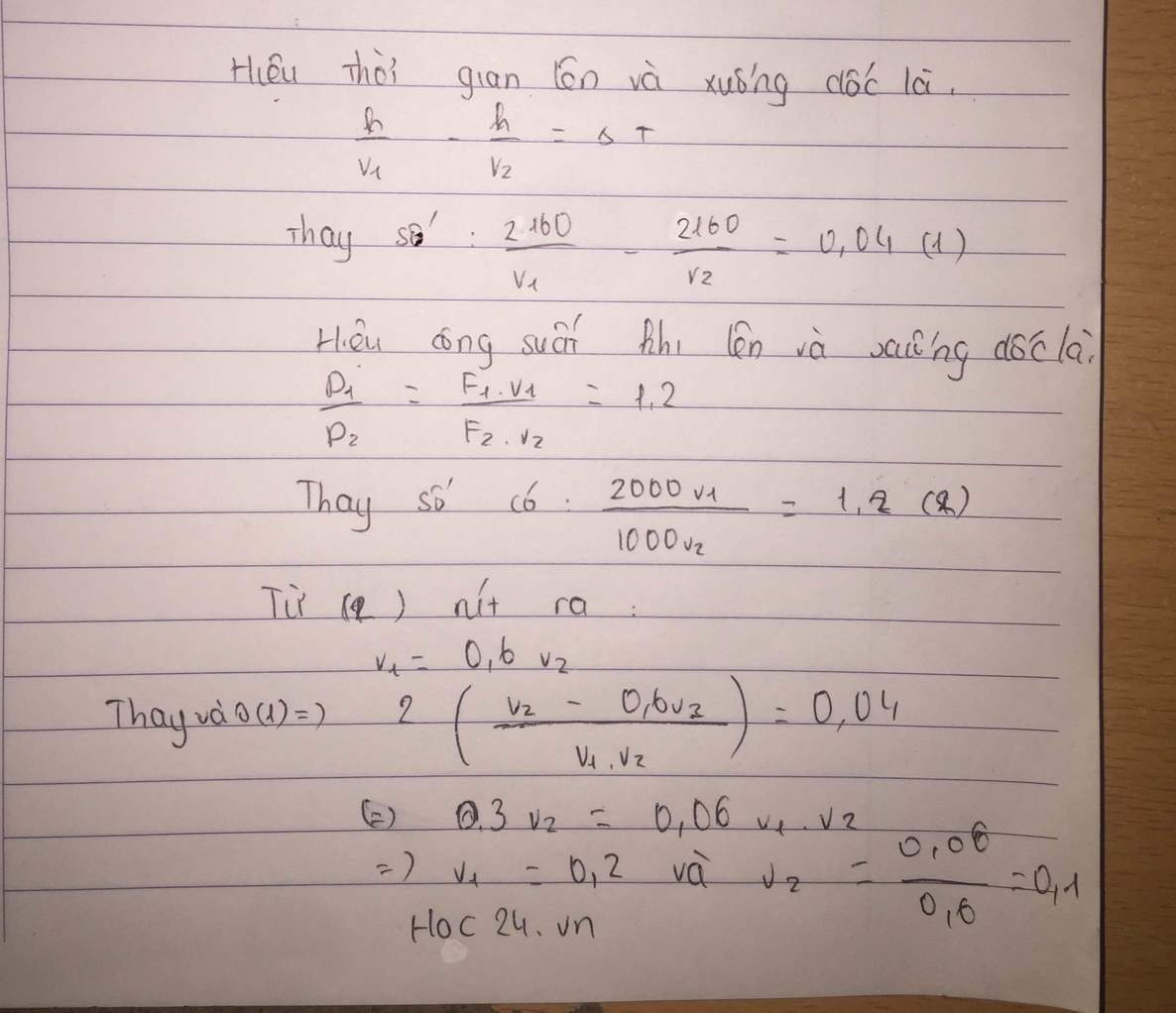
a)Gọi độ cao dốc là \(h\left(m\right)\).

Khi lên dốc xe có lực kéo \(F_1\) để thắng lực ma sát.

Định luật bảo toàn công:

\(F_1\cdot l=P\cdot h+F_{ms}\cdot l\)

\(\Rightarrow2500\cdot2\cdot1000=5\cdot1000\cdot10\cdot h+F_{ms}\cdot2\cdot1000\) (1)

Khi xe xuống dốc có lực kéo \(F_2\) tạo lực hãm.

Bảo toàn công: \(F_{ms}\cdot l-F_2\cdot l=P\cdot h\)

\(\Rightarrow F_{ms}\cdot2\cdot1000-500\cdot2\cdot1000=5\cdot1000\cdot10\cdot h\) (2)

Từ (1) và (2) giải hệ như bthg\(\Rightarrow\left\{{}\begin{matrix}F_{ms}=1500N\\h=40m\end{matrix}\right.\)

Vậy dốc cao 40m.

Answer 2

[nguyễn thị hương giang]

Bổ sung câu b):

Gọi vận tốc lúc len dốc và xuống dốc lần lượt là \(v_1;v_2\) (km/h)

Thời gian lúc lên dốc: \(t_1=\dfrac{L}{v_1}=\dfrac{2}{v_1}\left(h\right)\)

Thời gian lúc xuống dốc: \(t_2=\dfrac{L}{v_2}=\dfrac{2}{v_2}\left(h\right)\)

Thời gian lên dốc lớn hơn \(1,8'=\dfrac{3}{100}=0,03h\) thời gian lúc xuống dốc.

\(\Rightarrow t_1-t_2=\Delta t\Rightarrow\dfrac{2}{v_1}-\dfrac{2}{v_2}=0,03\left(1\right)\)

Biết công suất lên dốc lớn gấp 3,125 lần công suất lúc xuống dốc.

\(\Rightarrow\dfrac{P_1}{P_2}=\dfrac{F_1\cdot v_1}{F_2\cdot v_2}\Rightarrow\dfrac{2500\cdot v_1}{500v_2}=3,125\Rightarrow v_1=0,625v_2\left(2\right)\)

Thay (2) vào (1) ta được:

\(\dfrac{2}{0,625v_2}-\dfrac{2}{v_2}=0,03\Rightarrow v_2=40\)km/h

Vậy vận tốc xuống dốc là 40km/h

Và vận tốc lên dốc là \(v_1=0,625v_2=0,625\cdot40=25\)km/h