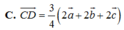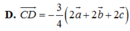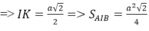cho tứ giác abcd gọi a' b' c' d' lần lượt là trọng tâm bcd;acd;abd,abc. chứng minh rằng các đường thẳng aa';bb';cc' đồng qui
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2018
a) G là trọng tâm của ABCD <=> vtGA + vtGB + vtGC + vtGD = vt0 (1*)
A' là trọng tâm của BCD <=> vtA'B + vtA'C + vtA'D = vt0
<=> 3.vtA'G + vtGB + vtGC + vtGD = vt0 (2*) (chen điểm G vào biểu thức trên)
lấy (1*) - (2*): vtGA - 3.vtA'G = vt0 <=> vtGA = 3.vtA'G
đẳng thức này chứng tỏ vtGA và vtA'G cùng hướng => G nằm trên đoạn AA'
tương tự có B' là trọng tâm của ACD <=> 3.vtB'G + vtGA + vtGC + vtGD = vt0 (3*)
lấy (1*) - (3*): vtGB - 3vtB'G = vt0 <=> vtGB = 3vtB'G
=> G nằm trên đoạn BB'
tiếp tục cho 2 phần còn lại
=> G là điểm chung của các đoạn AA', BB', CC', DD'
b) từ biểu thức trên có: vtGA = -3.vtGA'
=> G chia đoạn AA' theo tỉ số k = -3
các đoạn kia tương tự đều cùng tỉ số k = -3
c) từ cm trên ta có:
vtGA = -3vtGA'
vtGB = -3vtGB'
vtGC = -3vtGC'
vtGD = -3vtGD'
=> vtGA+vtGB+vtGC+vtGD+vtGD = -3(vtGA'+vtGB'+vtGC'+vtGD') (**)
mà G là trọng tâm của ABCD nên vtGA+vtGB+vtGC+vtGD = vt0
(**) => vtGA'+vtGB'+vtGC'+vtGD' = vt0 => G là trọng tâm của A'B'C'D'
5 tháng 11 2017
Gọi P và Q lần lượt là trung điểm của AC' và CA'.
CC' giao MN tại I
Xét tam giác AC'C. P là trung điểm AC', M là trung điểm của AC
=> PM là đường trung bình tam giác AC'C => PM//CC'
hay C'I//PM
C' là trọng tâm tam giác ABD => C'N=AN/3.(T/c trọng tâm)
Mà P là trung điểm AC' => C' là trung điểm PN.
Xét tam giác PNM: C' là trung điểm PN, C'I//PM => I là trung điểm của MN
=> CC' đi qua trung điểm của MN (1)
Tương tự ta chứng minh được AA' đi qua trung điểm MN (2)
Tương tự xét trong tam giác DMB: BB' và DD' cùng đi qua trung điểm I của MN (3)
Từ (1),(2) và (3) => AA';BB';CC';DD',MN đồng quy (đpcm).
13 tháng 7 2021
Bn ơi!
Chứng minh AA' đi qua trung điểm MN làm cách nào vậy ạ!
20 tháng 5 2017
nên \(V_{A'B'C'D'}=\dfrac{1}{27}V_{ABCD}=\dfrac{\sqrt{2}}{324}a^2\)
CM
20 tháng 6 2017
Chọn đáp án C
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: 
Khi đó: Giao tuyến = 
= Gx // CD