giải chi tiết bài này cho mk với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)

Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)

\(n_{Fe}=\dfrac{22,4}{56}=0,4\left(mol\right)\\
pthh:Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
0,4 0,4 0,4
\(V_{H_2}=0,4.22,4=8,96l\\
m_{FeCl_2}=0,4.127=50,8g\\
n_{Fe_2O_3}=\dfrac{14}{160}=0,0875\left(mol\right)\\
pthh:Fe_2O_3+3H_2\underrightarrow{t^o}2Fe+3H_2O\)
\(LTL:\dfrac{0,0875}{1}< \dfrac{0,4}{3}\)
=> H2 dư
\(n_{H_2\left(p\text{ư}\right)}=3n_{Fe_2O_3}=0,2625\left(mol\right)\\
m_{H_2\left(d\right)}=\left(0,4-0,2625\right).2=0,275g\\
n_{Fe}=2n_{Fe_2O_3}=0,175\left(mol\right)\\
m_{Fe}=0,175.56=9,8g\)

\(I=\int\dfrac{2}{2+5sinxcosx}dx=\int\dfrac{2sec^2x}{2sec^2x+5tanx}dx\\ =\int\dfrac{2sec^2x}{2tan^2x+5tanx+2}dx\)
We substitute :
\(u=tanx,du=sec^2xdx\\ I=\int\dfrac{2}{2u^2+5u+2}du\\ =\int\dfrac{2}{2\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{8}}du\\ =\int\dfrac{1}{\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{16}}du\\ \)
Then,
\(t=u+\dfrac{5}{4}\\I=\int\dfrac{1}{t^2-\dfrac{9}{16}}dt\\ =\int\dfrac{\dfrac{2}{3}}{t-\dfrac{3}{4}}-\dfrac{\dfrac{2}{3}}{t+\dfrac{3}{4}}dt\)
Finally,
\(I=\dfrac{2}{3}ln\left(\left|\dfrac{t-\dfrac{3}{4}}{t+\dfrac{3}{4}}\right|\right)+C=\dfrac{2}{3}ln\left(\left|\dfrac{tanx+\dfrac{1}{2}}{tanx+2}\right|\right)+C\)

\(\left\{{}\begin{matrix}6u_2+u_5=1\\3u_3+2u_4=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6u_1.q+u_1.q^4=1\\3u_1.q^2+2u_1.q^3=-1\end{matrix}\right.\)
\(\Rightarrow u_1\left(6q+q^4+3q^2+2q^3\right)=0\)
\(\Leftrightarrow q^3+2q^2+3q+6=0\)
\(\Leftrightarrow\left(q+2\right)\left(q^2+3\right)=0\)
\(\Leftrightarrow q=-\text{}2\)
\(\Rightarrow u_1=\dfrac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\dfrac{1}{4}.\left(-2\right)^{n-1}=\left(-2\right)^{n-3}\)

a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
b: \(MP=\sqrt{PK\cdot PN}=10\left(cm\right)\)

Ta có: \(n_{H_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
\(a.PTHH:\)
\(Mg+2HCl--->MgCl_2+H_2\left(1\right)\)
\(CuO+2HCl--->CuCl_2+H_2O\left(2\right)\)
b. Theo PT(1): \(n_{Mg}=n_{H_2}=0,25\left(mol\right)\)
\(\Rightarrow m_{Mg}=0,25.24=6\left(g\right)\)
\(\Rightarrow m_{CuO}=24,25-6=18,25\left(g\right)\)
c. Ta có: \(n_{CuO}=\dfrac{18,25}{80}=\dfrac{73}{320}\left(mol\right)\)
\(\Rightarrow n_{hh}=\dfrac{73}{320}+0,25=0,478125\left(mol\right)\)
Theo PT(1,2): \(n_{HCl}=2.n_{hh}=2.0,478125=0,95625\left(mol\right)\)
Đổi 300ml = 0,3 lít
\(\Rightarrow C_{M_{HCl}}=\dfrac{0,95625}{0,3}=3,1875M\)

program dung;
uses crt;
var x: integer'
t: real;
begin
clrscr;
write('x= '); readln(x);
t:=(5*x-7)+sqrt(3*x*x+7*x-6);
write('Dien tich la: ',s:1:2);
write('Ket qua: ',t);
readln;
end.
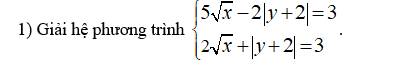

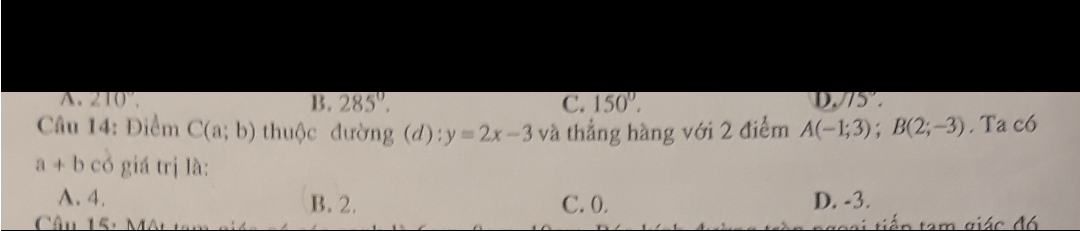






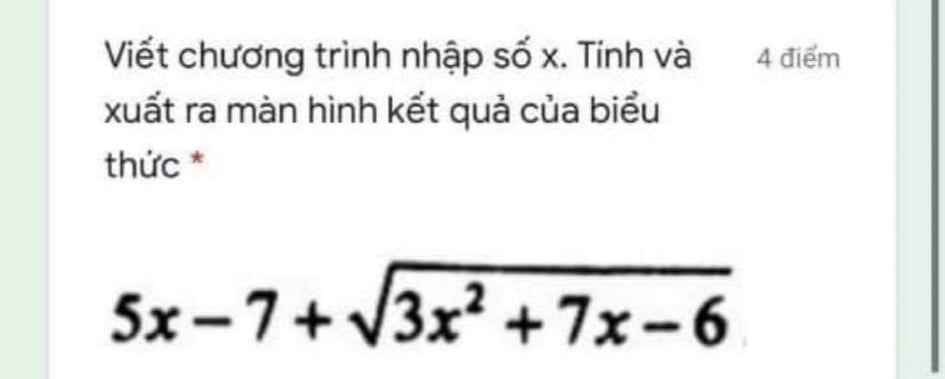
Giả sử \(x_1< x_2\)
Gọi A, B là 2 điểm biểu diễn \(x_1;x_2\) trên \(Ox\Rightarrow A\left(x_1;0\right)\) ; \(B\left(x_2;0\right)\)
\(OA=\left|x_1\right|;OB=\left|x_2\right|\)
\(\Rightarrow AB=\left|x_2-x_1\right|\)
Trong tam giác vuông OAN: \(OA^2+ON^2=AN^2\Rightarrow AN^2=x_1^2+b^2\)
Trong tam giác vuông OBN: \(OB^2+ON^2=BN^2\Rightarrow BN^2=x_2^2+b^2\)
Do tam giác ABN vuông tại N:
\(\Rightarrow AN^2+BN^2=AB^2\)
\(\Rightarrow x_1^2+x_2^2+2b^2=\left(x_2-x_1\right)^2\)
\(\Rightarrow2b^2=-2x_1x_2\Rightarrow b^2=-x_1x_2\)
\(\Rightarrow b^2=1011\Rightarrow b=\sqrt{1011}\)
Con cảm ơn thầy nhiều ạ