Chứng minh : x200+x100+1 chia hết cho x4+x2+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

28 tháng 7 2023
A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49
PT
1

CM
10 tháng 1 2017
Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 = 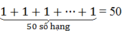
Vậy giá trị đa thức bằng 50 tại x = -1.

26 tháng 12 2021
\(=x^3\left(x+2\right)-x\left(x+2\right)\)
\(=\left(x+2\right)\cdot x\cdot\left(x+1\right)\left(x-1\right)\)
Vì đây là tích của bốn số nguyên liên tiếp
nên \(\left(x+2\right)\cdot x\cdot\left(x+1\right)\cdot\left(x-1\right)⋮24\)
vì x^200 chia hết cho 4 , x^100 chia hết cho x^2 và 1 chia hết cho 1 nên x^200+x^100+1 chia hếtcho x^4+x^2+1
**** bn nhe
Đặt x2=ax2=a. Cần chứng minh: a^100+a^50⋮a2+a+1a100+a50⋮a2+a+1
Sử dụng tính chất quen thuộc: a3m+1+a3n+2=a(a3m−1)+a2(a3n−1)−(a2+a+1)⋮a2+a+1