Cho tam giác ABC. Lấy điểm I nằm trong tam giác sao cho góc IBA = IBC. Gọi P là trung điểm BI. H là trung điểm CI. K là trung điểm BC. Vẽ IE vuông góc AB, IF vuông góc với AC
a. Cminh PIHK là hình bình hành
b. Cminh tam giác EFK là tam giác cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

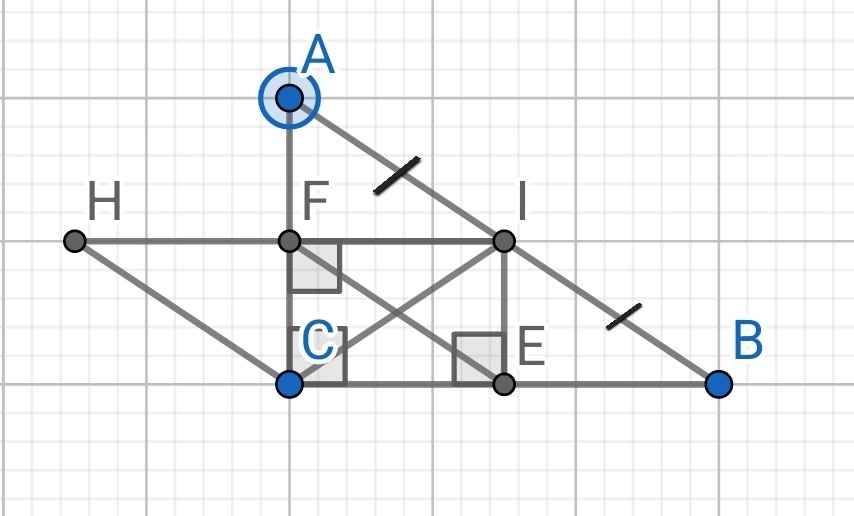 *) Tứ giác CEIF là hình gì?
*) Tứ giác CEIF là hình gì?
Tứ giác CEIF có:
∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)
⇒ CEIF là hình chữ nhật
*) Do CEIF là hình chữ nhật (cmt)
⇒ FI = CE và FI // CE
Do FI // CE (cmt)
⇒ FH // CE
Do FI = CE (cmt)
FI = FH (gt)
⇒ FH = CE
Tứ giác CHFE có:
FH // CE (cmt)
FH = CE (cmt)
⇒ CHFE là hình bình hành
Sửa đề: IF vuông góc AC tại F
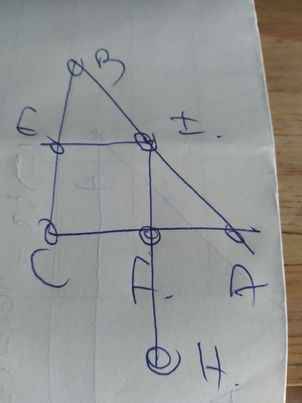
a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
b: CEIF là hình chữ nhật
=>CE//FI và CE=FI
CE=FI
FI=FH
Do đó: CE=FH
CE//FI
\(F\in IH\)
Do đó: CE=FH
Xét tứ giác CEFH có
CE//FH
CE=FH
Do đó: CEFH là hình bình hành

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
b: Xét tứ giác BECF có
I là trung điểm chung củaBC và EF
=>BECF là hình bình hành
=>BE//CF
=>CF vuông góc FI

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
b: Xét tứ giác BECF có
I là trung điểm chung củaBC và EF
=>BECF là hình bình hành
=>BE//CF
=>CF vuông góc FI