cho hình bình hành ABCD có AC > BD . Vẽ CE vuông góc với AB tại E và CF vuông góc với AD tại F . Biết đường chéo AC = a , hãy tính AB.AE + AD.AF theo a .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 6 2019
a,\(\Delta AHB\&\Delta AEC\)có: \(\widehat{A}chung,\widehat{AEC}=\widehat{AHB}=90^o\)
\(\Rightarrow\Delta AHB\infty\Delta AEC\left(g.g\right)\Rightarrow\frac{AH}{AE}=\frac{AB}{AC}\Rightarrow AB.AE=AH.AC\)
b,\(\Delta AKD\&\DeltaÀFC\)CÓ: \(\widehat{A}chung,\widehat{AFC}=\widehat{AKD}=90^o\)
\(\Rightarrow\Delta AKD\infty\DeltaÀFC\left(g.g\right)\Rightarrow\frac{AK}{AF}=\frac{AD}{AC}\Rightarrow AD.AF=AK.AC\)
c, Vì ABCD là hbh => AB=DC
--------------------- => AB//CD => GÓC BAC=ACD (SO LE TRONG)
Xét tam giác ABH và tam giác CDK có:
Tam giác ABH vuông tại H
----------- CDK ------------- K
cạnh huyền AB=CD
góc nhọn BAC=ACD
=> tam giác ABH = tam giác CDK
=> AH=KC
ta có: AC = AH + HC
Mà: AH=KC
=> AC = AH+HK+AH
=> AC = AH + AK
Ta có: AB.AE+AD.AF = AH.AC+AK.AC = AC.(AH+AK) = AC.AC = AC2
CM
3 tháng 7 2018
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: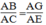 
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: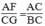 
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF = A C 2
NN
13 tháng 3 2022
Dựng BG ⊥ AC.
Xét ∆ BGA và ∆ CEA, ta có:
ˆBGA=ˆCEA=90∘BGA^=CEA^=90∘
ˆAA^ chung
Suy ra: ∆ BGA đồng dạng ∆ CEA (g.g)
Suy ra: ABAC=AGAEABAC=AGAE
Suy ra: AB.AE = AC.AG (1)
Xét ∆ BGC và ∆ CFA, ta có:
ˆBGC=ˆCFA=90∘;BGC^=CFA^=90∘
ˆBCG=ˆCAF;BCG^=CAF^ (so le trong vì AD // BC)
Suy ra: ∆ BGC đồng dạng ∆ CFA (g.g)
Suy ra: AFCG=ACBC⇒BC.AF=AC.CGAFCG=ACBC⇒BC.AF=AC.CG
Mà BC = AD (tính chất hình bình hành )
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế của đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
⇒AB.AE+AD.AF=AC(AG+CG)⇒AB.AE+AD.AF=AC(AG+CG)
Mà AG+CG=ACAG+CG=AC nên AB.AE+AD.AF=AC2
18 tháng 2 2021
Ta chứng minh
Tương tự câu a ta chứng minh được
Þ AD.AF =AK.AC (2)
Từ (1) ta có AB.AE = AC.AH (3)
Lấy (3) + (2) ta được AD.AF + AB.AE = AC2 (ĐPCM)
MT
1
25 tháng 2 2019
Câu hỏi của Nguyễn Đình Kim Thanh - Toán lớp 8 - Học toán với OnlineMath
Em xem link bài nhé!
KT
29 tháng 4 2018
Từ D kẻ DH vuông góc với AC (H thuộc AC)
Xét \(\Delta AHD\)và \(\Delta AFC\:\)có:
\(\widehat{AHD}=\widehat{AFC\:}=90^0\)
\(\widehat{HAD}\) chung
suy ra: \(\Delta AHD~\Delta AFC\:\)
\(\Rightarrow\)\(\frac{AH}{AF}=\frac{AD}{AC}\)
\(\Rightarrow\)\(AD.AF=AH.AC\) (1)
Xét \(\Delta AEC\) và \(\Delta CHD\) có:
\(\widehat{AEC}=\widehat{CHD}=90^0\)
\(\widehat{EAC}=\widehat{HCD}\) (slt do ABCD là hình bình hành nên AB//CD)
suy ra: \(\Delta AEC~\Delta CHD\)
\(\Rightarrow\)\(\frac{AE}{CH}=\frac{AC}{CD}\)
\(\Rightarrow\)\(AE.CD=CH.AC\)
mà \(CD=AB\) (do ABCD là hình bình hành)
\(\Rightarrow\)\(AB.AE=CH.AC\)
Lấy (1) + (2) theo vế ta được:
\(AD.AF+AB.AE=AH.AC+HC.AC=AC^2\) (đpcm)
25 tháng 3 2021
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: 
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: 
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG