Cho hình thoi MNPQ có O là giao điểm của hai đường chéo. Biết ON = 9cm, OM= 12cm. Diện tính hình thoi MNPQ là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 1 2022
\(MNPQ\) là hình thoi, \(MP\) ∩ \(NQ\) \(=\) {\({Q}\)}
\(\rightarrow MP\) ⊥ \(PQ\) tại \(O\)
\(\rightarrow OP=OM,OQ=ON\)
Áp dụng định lý Pytago vào \(△ MON\) vuông tại \(O\)
\(\rightarrow MN^2=MO^2+ON^2\)
\(\Leftrightarrow 10^2=3^2+ON^2\)
\(\Leftrightarrow 100=9+ON^2\)
\(\Leftrightarrow ON^2=91\)
\(\Leftrightarrow ON=\sqrt{91}\)
\(\rightarrow QN=2\sqrt{91}\)
Lại có : \(MP=6\) cm
\(\rightarrow S_{MNPQ}=\dfrac{1}{2}.2\sqrt{91}.6=6\sqrt{91}\) (\(cm^2)\)
31 tháng 8 2016
Chu vi của hình thoi là:
120 : 2 = 60(m)
Tổng hai cạnh của hình thoi là:
60 : 2 = 30(m)
Độ
8 tháng 7 2023
a) (hình tự vẽ)
Độ dài của đường chéo NQ là: \(2,4\cdot\dfrac{5}{8}=1,5\left(m^2\right)\)
Diện tích tấm bạt: \(\dfrac{1,5\cdot2,4}{2}\)= 1,8 (m2)
b) Độ dài của đoạn thẳng MO: 2,4 : 2=1,2(m)
___________________ AO: 1,2 : 2 =0,6 (m)
Diện tích của tam giác QAN: \(\dfrac{1,5\cdot0,6}{2}=0.45\left(m^2\right)\)
c) Đổi: 1,8 m2 = 180 dm2
Tấm bạt có giá: (180 : 5 ) * 3500 = 126000 (đồng)
CM
15 tháng 5 2018
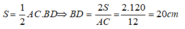
Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD.
Suy ra:
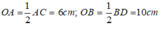
Áp dụng định lí Pytago vào tam giác OAB có:
A B 2 = O A 2 + O B 2 = 6 2 + 10 2 = 136
⇒ A B = 2 34 c m
Chọn đáp án B
25 tháng 3 2022
Tổng độ dài hai đường chéo hình thoi là:
120 : 2 = 60 (cm)
Sơ đồ bài toán tổng - hiệu: Hình bên dưới.
Độ dài đường chéo 1 của hình thoi là:
(60 + 12) : 2 = 36 (cm)
Độ dài đường chéo 2 của hình thoi là:
60 - 36 = 24 (cm)
Diện tích hình thoi MNPQ là:
36×24/2 = 432 (cm²)
Đáp số: 432 cm²
22 tháng 2 2023
Độ dài đường chéo 1 là (84+12)/2=96/2=48(cm)
Độ dài đường chéo 2 là 48-12=36(cm)
Diện tích là 48*36/2=48*18=864(cm2)
Chiều cao là 864:30=28,8(cm)
B. Diện tích hình thoi lớn hơn diện tích hình vuông đúng/sai 
C. Diện tích hình thoi bé hơn diện tích hình vuông đúng/ sai
Diện tích hình thoi MNPQ là:
\(\dfrac{9\times12}{2}=54\left(cm^2\right)\)
Đ.s 54 cm2