Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi hình thoi đó là ABCD
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH (H\(\in DC\))
a. SABCD=\(\dfrac{1}{2}.AC.BD=\dfrac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là 96 cm2
b. Ta có: AO=OC=\(\dfrac{AC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
OD=OB=\(\dfrac{BD}{2}=\dfrac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\) có \(\widehat{DOA}=90^o\)
=> OD2+AO2=AD2 (định lý Py-ta-go)
hay: 82+62=AD2
=> AD2=100
=> AD=10 (cm)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c. Ta có: SABCD=AH.DC
=> AH=\(\dfrac{S_{ABCD}}{DC}=\dfrac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài đường cao của hình thoi đó là 9,6 cm

Gọi hình thoi đó là \(ABCD\)
Hai đường chéo BD và AC cắt nhau và vuông góc tại O
Kẻ đường cao AH \(\left(H\in DC\right)\)
a ) \(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.12.16=96\left(cm^2\right)\)
Vậy diện tích hình thoi đó là \(96cm^2\)
b ) Ta có : \(AO=OC=\frac{AC}{2}=\frac{12}{2}=6\left(cm\right)\)
\(OD=OB=\frac{BD}{2}=\frac{16}{2}=8\left(cm\right)\)
Xét \(\Delta DAO\)có \(\widehat{DOA}=90^0\)
\(\Rightarrow OD^2+AO^2=AD^2\)( định lí Py - ta - go )
Hay \(8^2+6^2=AD^2\)
\(\Rightarrow AD^2=100\)
\(\Rightarrow AD=10\left(cm\right)\)
Vậy độ dài một cạnh của hình thoi đó là 10 cm
c ) Ta có : \(S_{ABCD}=AH.DC\)
\(\Rightarrow AH=\frac{S_{ABCD}}{DC}=\frac{96}{10}=9,6\left(cm\right)\)
Vậy độ dài dduwowgf cao của hình thoi là 9,6 cm
Chúc bạn học tốt !!!

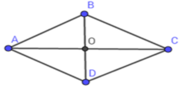
Ta có: AC = 2AO = 2.12 = 24cm
SABCD = 1 2 BD.AC
=> BD = 2 S A B C D A C = 2.168 24 =14(cm)
=> BO = 1 2 BD = 1 2 .14 = 7(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)
Đáp án cần chọn là: C

a: Xét tứ giác MBNC có
MB//NC
NB//MC
Do đó: MBNC là hình bình hành
mà \(\widehat{BMC}=90^0\)
nên MBNC là hình chữ nhật
b: Ta có: MBNC là hình chữ nhật
nên MN=BC
mà BC=AB
nên MN=AB

Do \(ABCD\) là hình thoi nên hai đường chéo vuông góc với nhau tạo ra 4 góc vuông.
Áp dụng ĐL Pythagore vào 1 trong các tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{6}{2}} \right)}^2} + {{\left( {\frac{8}{2}} \right)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\) (cm)

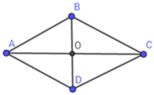
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, AB = 5 cm; BD = 6 cm.
Suy ra BO = 1 2 BD = 1 2 .6 = 3 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AO = A B 2 − O B 2 = 5 2 − 3 2 = 4
SABCD = 1 2 BD. AC = 1 2 BD. 2AO = BD.AO = 6.4 = 24 (cm2)
Đáp án cần chọn là: C

Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD.
Suy ra:
Áp dụng định lí Pytago vào tam giác OAB có:
A B 2 = O A 2 + O B 2 = 6 2 + 10 2 = 136
⇒ A B = 2 34 c m
Chọn đáp án B