Cho TKHT có OF=OF'=18cm OA=d=12cm AB=h=2cm
a, trình bày cách dựng và nêu tính chất của ảnh
b,CMR nếu d<f thì h/h’= d/d’ và 1/f= 1/d – 1/d’
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2021
b)
Tóm tắt:
AB = 2cm
OF = OF' = 8cm
OA = 24cm
A'B' = ?
OA' = ?
Giải:
\(\Delta ABF\sim OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{2}{A'B'}=\dfrac{24-8}{8}\)
=> A'B' = 1cm
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{24}{OA'}=\dfrac{2}{1}\Rightarrow OA'=12cm\)
7 tháng 2 2022
a)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{8}+\dfrac{1}{d'}\Rightarrow d'=24cm\)
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{8}{24}\Rightarrow h'=9cm\)
b)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{12}+\dfrac{1}{d'}\Rightarrow d'=12cm\)
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{12}{12}\Rightarrow h'=3cm\)
c)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{4}+\dfrac{1}{d'}\Rightarrow d'=-12cm\)
\(\Rightarrow TH\) không xảy ra.
d)\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{18}+\dfrac{1}{d'}\Rightarrow d'=9cm\)
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{18}{9}\Rightarrow h'=1,5cm\)
7 tháng 2 2022
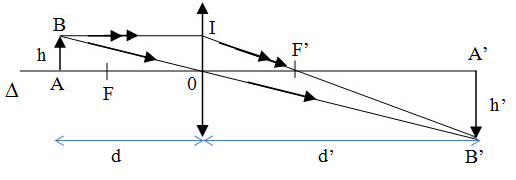
Hình vẽ thì em tham khảo nhé!
Áp dụng công thức: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\) và độ cao ảnh \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
a) \(\dfrac{1}{6}=\dfrac{1}{8}+\dfrac{1}{d'}\Rightarrow d'=24cm\)
Độ cao ảnh: \(\dfrac{h}{h'}=\dfrac{8}{24}=\dfrac{1}{3}\)
Đề không cho độ cao vật nên chị làm đến đây, nếu có cho thì em thay vào h rồi tính h' là chiều cao ảnh cần tìm
28 tháng 4 2017
a)hình bạn tự vẽ nha chứ mik vẽ lâu lắm
b)ta có:
\(\Delta\)OAB đồng dạng với \(\Delta\)OA'B':
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\)
\(\Delta\)OIF' đồng dạng với \(\Delta\)A'B'F'
\(\Rightarrow\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\)
\(\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow OA.OA'-OA.OF'=OF'.OA'\)
chia hai về cho OA.OA'.OF'
\(\Rightarrow\dfrac{1}{OF}-\dfrac{1}{OA'}=\dfrac{1}{OA}\)
mà OA=2OF'\(\Rightarrow OF'=0,5OA\)
\(\Rightarrow\dfrac{1}{0,5OA}-\dfrac{1}{OA'}=\dfrac{1}{OA}\)
\(\Leftrightarrow\dfrac{1}{0,5OA}-\dfrac{1}{OA}=\dfrac{1}{OA'}\)
\(\Leftrightarrow\dfrac{2}{OA}-\dfrac{1}{OA}=\dfrac{1}{OA'}\)
\(\Leftrightarrow\dfrac{1}{OA}=\dfrac{1}{OA'}\Rightarrow OA=OA'\)
c)ta có:
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\)
\(\Leftrightarrow\dfrac{h}{h'}=\dfrac{OA}{OA'}\)
mà OA=OA' nên:
\(\dfrac{h}{h'}=1\Rightarrow h=h'\)
d)ta có:
\(\dfrac{1}{OF'}=\dfrac{1}{OA'}+\dfrac{1}{OA}\)
mà OA=OA' nên:
\(\dfrac{1}{f}=\dfrac{2}{OA}\)
\(\Rightarrow f=\dfrac{OA}{2}=\dfrac{OA'}{2}\)
TM
0
