Một bình nhiệt lượng kế chứa nước ở nhiệt độ t =200C; người ta thả vào trong bình này những quả cầu giống nhau đã được đốt nóng đến 1000C. Sau khi thả quả cầu thứ nhất nhiệt độ của nước trong bình khi cân bằng nhiệt là t1 = 400C. Nhiệt độ của nước trong bình khi cân bằng nhiệt là bao nhiêu khi thả quả cầu thứ 2, thứ 3? Cần bao nhiêu quả cầu để nhiệt độ của nước trong bình khi cân bằng nhiệt là 900C? Bỏ qua sự trao đổi nhiệt với thành bình và môi trường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, lần 1 cho quả cân vào bình B, cân bằng ta có \(m_2C_2\left(74-24\right)=m_3C_1\left(24-20\right)\left(1\right)\)
lần 2 cho quả cân bình A
\(m_2C_2.\left(72-24\right)=m_1C_1.\left(74-72\right)\left(2\right)\)
chia 2 vế (1) cho (2)
\(\dfrac{50}{48}=4m_3\Rightarrow m_3\approx0,26\left(kg\right)\)
b, lần 3 cho cân lại bình B
\(m_2C_2\left(72-x\right)=m_3C_1\left(x-24\right)\left(3\right)\)
chia 2 vế (3) cho (1) \(\Rightarrow x=27,5^oC\)

Nhiệt lượng do 10g hơi nước tỏa ra khi nguội đến t = 400
Q 1 = L m 1 + c m 1 ( 100 − 40 ) = L m 1 + 60 c m 1 (1)
Nhiệt lượng do nước trong nhiệt lượng kế hấp thụ: Q 2 = c m 2 ( 40 − 20 ) = 20 c m 2 (2)
Nhiệt lượng do nhiệt lượng kế hấp thụ: Q 3 = q : ( 40 − 20 ) = 20 q (3)
Theo định luật bảo toàn năng lượng ta có: Q1 = Q2 + Q3
L m 1 + 60 c m 1 = 20 c m 2 + 20 q ⇒ L = 20 c m 2 − 60 c m 1 + 20 q m 1 ⇒ L = 20 c ( m 2 − 3 m 1 ) + 20 q m 1 = 20.4 , 18.260 + 4 , 6.20 10 ⇒ L = 2173 , 6 + 92 = 2265 , 6 J / g

\(Qthu\)(nước bình 2)\(=m.Cn.\left(t2-20\right)=2.4200.\left(t2-20\right)\left(J\right)\)
\(Qtoa\)(nước bình 1)\(=m1.Cn.\left(60-t2\right)=4200.m1\left(60-t2\right)\left(J\right)\)
\(=>2.4200\left(t2-20\right)=4200m1\left(60-t2\right)\)
\(=>2\left(t2-20\right)=m1\left(60-t2\right)\left(1\right)\)
*khi có cân bằng nhiệt lại rótlượng nước như cũ từ bình 2 sang bình 1. Khi đó nhiệt độ bình 1 là 580C
\(Qth\)u(nước bình 2 rót sang)\(=m1.Cn.\left(58-t2\right)=4200m1\left(58-t2\right)\)(J)
\(Qtoa\)(nuosc bình 1)\(=\left(10-m1\right).Cn.\left(60-58\right)=\left(10-m1\right).4200.2\left(J\right)\)
\(=>4200m1\left(58-t2\right)=4200\left(10-m1\right).2\)
\(=>m1\left(58-t2\right)=2\left(10-m1\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\)=>hệ pt: \(\left\{{}\begin{matrix}2\left(t2-20\right)=m1\left(60-t2\right)\\m1\left(58-t2\right)=2\left(10-m1\right)\end{matrix}\right.\)
giải hệ trên \(=>\left\{{}\begin{matrix}m=\dfrac{2}{3}kg\\t2=30^oC\end{matrix}\right.\)
Vậy..............
b, có:
\(Qtoa=10.Cn.\left(60-t\right)\left(J\right)\)
\(Qthu=2.4200\left(t-20\right)\left(J\right)\)
\(=>10.4200.\left(60-t\right)=2.4200.\left(t-20\right)=>t\approx53,3^0C\)

Khi được làm lạnh tới 00C, nước toả ra một nhiệt lượng bằng: Q1 = m1.C1(t – 0) = 0,5.4200.20 = 42 000JĐể làm “nóng” nước đá tới 00C cần tốn một nhiệt lượng:Q2 = m2.C2(0 – t2) = 0,5.2100.15 = 15 750JBây giờ muốn làm cho toàn bộ nước đá ở 00C tan thành nước cũng ở 00C cần một nhiệt lượng là: Q3 = λ.m2 = 3,4.105.0,5 = 170 000JNhận xét:+ Q1 > Q2 : Nước đá có thể nóng tới 00C bằng cách nhận nhiệt lượng do nước toả ra+ Q1 – Q2 < Q3 : Nước đá không thể tan hoàn toàn mà chỉ tan một phần.Vậy sau khi cân bằng nhiệt được thiết lập nước đá không tan hoàn toàn và nhiệt độ của hỗn hợp là 00C

Tóm tắt
\(m_1=500g=0,5kg\)
\(t_1=13^0C\)
\(m_2=400g=0,4kg\)
\(t_2=100^0C\)
\(t=20^0C\)
\(c_1=4200J/kg.K\)
_____________
\(Q_1=?\)
\(c_2=?\)
Giải
Nhiệt lượng của nước thu vào là:
\(Q_1=m_1.c_1.\left(t-t_1\right)=0,5.4200.\left(20-13\right)=14700\left(J\right)\)
Nhiệt lượng của miếng kim loại toả ra là:
\(Q_2=m_2.c_2.\left(t_2-t\right)=0,4.c_2.\left(100-20\right)=32c_2\left(J\right)\)
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\)
\(\Leftrightarrow14700=32c_2\)
\(\Leftrightarrow c_2=459,4J/kg.K\)

Ta có phương trình cân bằng nhiệt lần 1
\(Q_{tỏa}=Q_{thu}\\ \Leftrightarrow4c\left(60-t_{cb_1}\right)=mc\left(t_{cb_1}-20\right)\\ \Leftrightarrow240-4t_{cb_1}=mt_{cb_1}-20m\\ \Leftrightarrow t_{cb_1}=\dfrac{240+20m}{m+4}\left(1\right)\)
Ta có phương trình cân bằng nhiệt lần 2
\(Q_{tỏa}=Q_{thu}\\ \Leftrightarrow mc\left(t_{cb_1}-21,95\right)=2-mc.1,95\\ \Leftrightarrow mt_{cb_1}=3,9-1,95m+21,95m\\ \Leftrightarrow t_{cb_1}=\dfrac{3,9+20m}{m}\left(2\right)\)
Từ (1) và (2)
\(\dfrac{240+20m}{m+4}=\dfrac{3,9+20m}{m}\Rightarrow240m+20m^2=3,9m+20m^2+15,6+80m\\ \Leftrightarrow m\approx0,1\)

Đáp án: D
- Nhiệt lượng mà nhiệt lượng kế thu vào:
![]()
- Nhiệt lượng nước thu vào:
![]()
- Nhiệt lượng đồng tỏa ra:
![]()
- Theo phương trình cân bằng nhiệt ta có: Q = Q 1 + Q 2
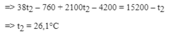
a, Gọi khối lượng nước là \(m\), khối lượng và nhiệt dung riêng quả cầu là \(m_1,c_1\). Nhiệt độ khi cân bằng nhiệt là \(t_{cb}\left(tcb\right)\) và số quả cầu thả vô nước là \(N\)
Ta có
Nhiệt lượng từ các quả cầu là
\(Q_{tỏa}=Nm_1c_1\left(100-t_{cb}\right)\)
Nhiệt lượng cân bằng của nước là
\(Q_{thu}=4200m\left(t_{cb}-20\right)\)
Pt cân bằng :
\(Q_{thu}=Q_{tỏa}\\ \Leftrightarrow4200m\left(t_{cb}-20\right)=Nm_1c_1\left(100-t_{cb}\right)\left(1\right)\)
Khi thả quả cầu đầu tiên \(N=1;t_{cb}=40^oC\) ta có
\(1m_1c_1\left(100-40\right)=4200m\left(40-20\right)\\ \Rightarrow m_1c_1=1400m\left(2\right)\)
Thay (2) và (1) ta đc
\(N.1400m\left(100-t_{cb}\right)=4200m\left(t_{cb}-20\right)\\ \Rightarrow100N-Nt_{cb}=3t_{cb}-60\left(\cdot\right)\)
Khi thả thêm quả cầu thứ 2 \(N=2\), từ pt \(\left(\cdot\right)\) ta được
\(200-2t_{cb}=3t_{cb}-60\\ \Rightarrow t_{cb}=52^oC\)
Vậy khi thả thêm quả cầu thứ 2 thì nhiệt độ cân bằng của nước là 52oC
Khi thả thêm quả cầu thứ 3 \(N=3\) từ pt \(\left(\cdot\right)\) ta đc
\(300-3t_{cb}=3t_{cb}-60^oC\Rightarrow t_{cb}=60^oC\)
Vậy khi thả thêm quả cầu thứ 3 thì \(t_{cb}\) nước là 60oC
Khi \(t_{cb}=90^oC\) từ pt \(\left(\cdot\right)\) ta đc
\(100N-90N=270-60\\ \Rightarrow N=21\)
Vận cần thả 21 quả cầu thì \(t_{cb}=90^oC\)