Cho parabol(P):y= x^2 và đường thẳng(d):y=x+2
a)Vẽ đồ thị 2 hàm số trên,trên cùng 1 hệ trục toạ độ
b) Xác định toạ độ giao điểm A,B của 2 đồ thị trên
c) Cho điểm M thuộc Parabol(P) có hoành độ là m nhỏ thoả mãn
-1 ≤m ≤2. Chứng minh Diện tích MAB ≤ 27/8

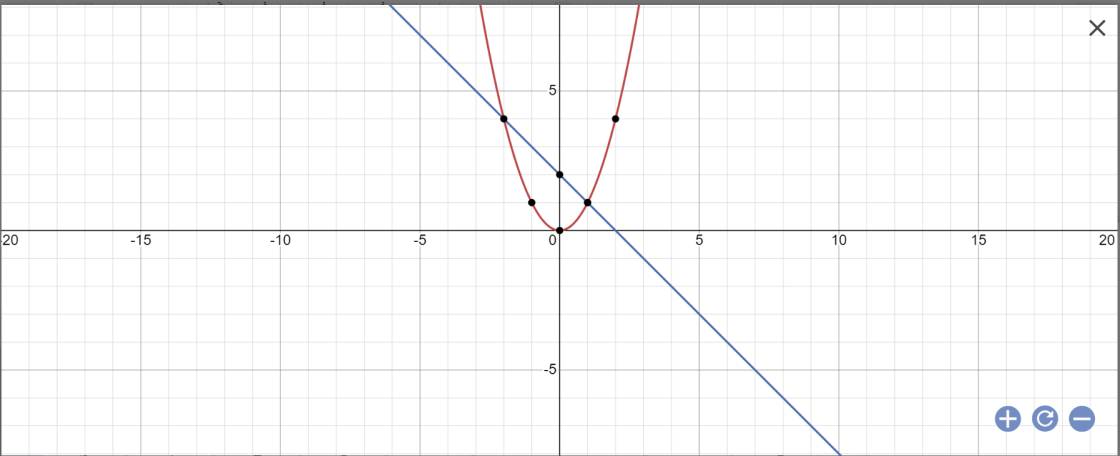
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)