Từ điểm A nằm ngoài (O; R) (OA > 2R), vẽ hai tiếp tuyến AB, AC với (O) (B, C là
hai tiếp điểm).
a/ Chứng minh tứ giác ABOC nội tiếp và OA vuông góc với BC tại H.
b/ Gọi M là trung điểm AC, BM cắt (O) tại E. Chứng minh MC2 = ME.MB và \(\widehat{MAE}\) = \(\widehat{MBA}\)
em chỉ cần ý 2 của câu b thôi ạ. xin giúp e với:<<





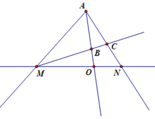
b: MC^2=ME*MB
=>MA^2=ME*MB
=>MA/ME=MB/MA
Xét ΔMAB và ΔMEA có
MA/ME=MB/MA
góc AMB chung
=>ΔMAB đồng dạng với ΔMEA
=>góc MAE=góc MBA