cho tam giác nhọn abc kẻ ah vuông góc với bc biết ac=20cm ah=12cm bh=16cm tính chu vi tam giác abc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)

Theo gt ta có : AH vuông góc với BC
=> \(\Delta\) AHB và \(\Delta\) AHC là \(\Delta\) vuông
Xét : \(\Delta\) AHB có : AH\(^2\)+ HB\(^2\) = AB\(^2\)
mà : AH = 12cm, HB = 5cm
=> AB\(^2\)= 12\(^2\)+ 5\(^2\)
=> AB\(^2\)= 144 + 25
=> AB\(^2\)= 169
=> AB = 13 cm (1)
Tương tự ta cũng có :
=> AC\(^2\)= 12\(^2\)+ 16\(^2\)
=> AB\(^2\)= 144 + 256
=> AB\(^2\)= 400
=> AB = 20 cm (2)
Mặt khác : BC = BH + CH
=> BC = 5 + 16 = 21cm (3)
Từ : (1), (2), (3) => chu vi tam giác ABC = 13 + 20 + 21 = 54 cm

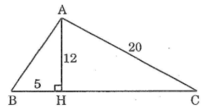
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

A B H C
Xét \(\Delta\)AHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = \(\sqrt{256}\) = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét \(\Delta\)AHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = \(\sqrt{169}\) = 13 (cm)
Chu vi của \(\Delta\)ABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của \(\Delta\)ABC là 54 cm.

\(AB^2=AH^2+BH^2\)
\(AB=12^2+5^2=169\)
\(AB=\sqrt{169}=13\left(cm\right)\)
▲AHC vuông tại H ta có:
HC\(^2\)=\(AC^2-AH^2\)=\(20^2-12^2\)=256
\(\)Chu vi ▲ABC là:
AB+BC+AC=AB+BH+HC+AC=\(13+5+16+20=54\left(cm\right)\)
Tham khảo:
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)

a) Xét ΔAHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(AB^2=AH^2+HB^2\)
\(\Rightarrow AB=\sqrt{AH^2+HB^2}\)
\(\Rightarrow AB=\sqrt{12^2+5^2}=13\left(cm\right)\)
b) Xét ΔAHC vuông tại H áp dụng định lý Py-ta-go ta có:
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{20^2-12^2}=16\left(cm\right)\)
\(\Rightarrow BC=HB+HC=5+16=21\left(cm\right)\)
\(\Rightarrow C_{ABC}=BC+AB+AC=21+13+20=54\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Ta có: BH+HC=BC(H nằm giữa B và C)
nên BC=16+16=32(cm)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+BC+AC=20+32+20=72\left(cm\right)\)
Lời giải:
Áp dụng định lý Pitago cho tam giác $AHC$ vuông tại $H$:
$HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
Áp dụng định lý Pitago cho tam giác $AHB$ vuông tại $H$:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20$ (cm)
Chu vi tam giác $ABC$:
$AB+BC+AC=AB+BH+CH+AC=20+16+16+20=72$ (cm)