cho tam giác ABC,trung tuyến AK,CL.gọi P là điểm bất kì trên AC.Kẻ đương thẳng //AK,CL qua P cắt BC tại E,AB tại F.CMR:AK,CL chia EF làm ba phần bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 12 2019
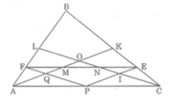
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL
Trong △ FPE ta có: PE//AK hay QM //PE
Suy ra: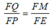 
(định lí ta-lét) (1)
Trong △ ALO ta có:PF //CL hay FQ //LO
Suy ra: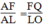
(định lí ta-lét) (2)
Trong △ ALC ta có: PF // CL
Suy ra: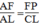 
(định lí ta-lét) (3)
Từ (2) và (3) suy ra: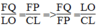 
Vì LO = 1/3 CL (O giao điểm của hai đường trung tuyến) nên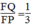 
(4)
Từ (1) và (4) suy ra: 
⇒ FM = 1/3 FE
Trong △ EPF ta có:PF // CL hay NI // PF
Suy ra: 
(định lí ta –lét) (5)
Trong △ CKO ta có: EI // OK
Suy ra: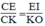 
(định lí ta –lét) (6)
Trong △ CKA ta có:PE // AK
Suy ra: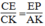 
(định lí ta –lét) (7)
Từ (6) và (7) suy ra: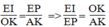 
Vì OK = 1/3 AK (O là giao điểm của hai đường trung tuyến) nên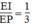 
(8)
Từ (5) và (8) suy ra: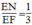 
⇒EN = 1/3 EF
Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF
Vậy EN = MN = NF
10 tháng 5 2023
Gọi H là giao của PF và AK, I là giao của PE và CN
Xét ΔFPE có PE//AK
=>HM//PE
=>FH/FB=FM/FE
Xét ΔANO có PF//CN
=>FH//NO
=>AF/AN=FH/NO
ΔALC có PF//CN
nên AF/AN=FP/CN
=>FH/NO=FP/CN
=>FH/EP=NO/CN
NO=1/3CN
nên FH/FP=1/3
=>FM/FE=1/3
=>FM=1/3FE
PF//CN
=>QI//PF
=>EI/EP=EQ/EF
EI//OK
=>CE/CK=EI/KO
PE//AK
=>CE/CK=EP/AK
=>EI/OK=EP/AK
=>EI/EP=OK/AK=1/3
=>EQ=1/3EF
=>FM=MQ=QE