Cho \(\Delta\)ABC cân tại A có đường cao AH , I là trung điểm AB , K đối xứng H qua I
a) Biết AB = 6cm. Tính IH
b) CM: AHBK là HCN
c) Tam giác ABC có thêm điều kiện gì thì HCN AHBK là Hình vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
26 tháng 11 2023
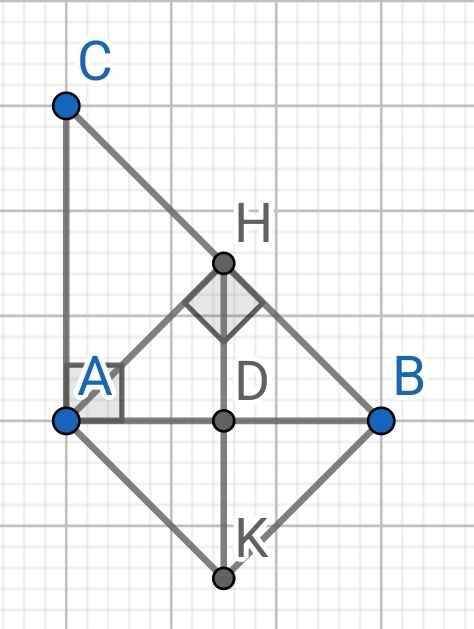
Do AH ⊥ BC (gt)
⇒ AH ⊥ BH
Do ∆ABC vuông cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Gọi D là giao điểm của AB và HK
Do H và K đối xứng nhau qua AB (gt)
⇒ D là trung điểm của HK và AB là đường trung trực của HK
⇒ HK ⊥ AB
Mà AB ⊥ AC
⇒ HK // AC
⇒ HD // AC
Mà H là trung điểm của BC
⇒ D là trung điểm AB
Do ∆ABC vuông cân tại A (gt)
AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH = HB = HC = BC : 2
Tứ giác AHBK có:
D là trung điểm HK (cmt)
D là trung điểm AB (cmt)
⇒ AHBK là hình bình hành
Mà AH ⊥ BH (cmt)
⇒ AHBK là hình chữ nhật
Lại có AH = BH (cmt)
⇒ AHBK là hình vuông
13 tháng 1 2022
a: Xét tứ giác AHBK có
M là trung điểm của AB
M là trung điểm của HK
Do đó: AHBK là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBK là hình chữ nhật
b:
Xét tứ giác AKHC có
AK//HC
AK=HC
Do đó: AKHC là hình bình hành
c: Xét ΔABC có
N là trung điểm của AC
H là trung điểm của BC
Do đó: NH là đường trung bình
=>NH//AB và NH=AB/2
hay NH//AM và NH=AM
=>AMHN là hình bình hành
mà AM=AN
nên AMHN là hình thoi
31 tháng 12 2023
a: Ta có: ΔBAC cân tại B
mà BI là đường cao
nên I là trung điểm của AC
Xét tứ giác BICD có
H là trung điểm chung của BC và ID
=>BICD là hình bình hành
Hình bình hành BICD có \(\widehat{BIC}=90^0\)
nên BICD là hình chữ nhật
b: Ta có: ΔBDC vuông tại D
=>\(BD^2+DC^2=BC^2\)
=>\(BD^2=14^2-10^2=96\)
=>\(BD=4\sqrt{6}\left(cm\right)\)
Vì BDCI là hình chữ nhật
nên \(S_{BDCI}=BD\cdot DC=4\sqrt{6}\cdot10=40\sqrt{6}\left(cm^2\right)\)
c: Để hình chữ nhật BDCI là hình vuông thì BI=CI
mà CI=CA/2
nên BI=CA/2
Xét ΔBAC có
BI là đường trung tuyến
\(BI=\dfrac{AC}{2}\)
Do đó: ΔBAC vuông tại B
=>\(\widehat{ABC}=90^0\)
PA
16 tháng 11 2016
SABC = \(\frac{4\times6}{2}\) = 12 (cm2)
BH là đường cao của tam giác BAC cân tại B.
=> BH là đường trung tuyến của tam giác ABC.
=> H là trung điểm của AC.
=> AH = HC = AC/2 = 6/2 = 3 (cm)
Tam giác HBC vuông tại H có:
BC2 = HB2 + HC2 (định lý Pytago)
= 42 + 32
= 16 + 9
= 25
BC = \(\sqrt{25}\) = 5 (cm)
Tam giác HBC vuông tại H có HI là đường trung tuyến (I là trung điểm của BC)
=> HI = BC/2 = 5/2 = 2,5 (cm)
I là trung điểm của BC (gt)
I là trung điểm của HD (H đối xứng D qua I)
=> BHCD là hình bình hành.
mà BHC = 900
=> BHCD là hình chữ nhật.
=> BHCD là hình vuông
<=> BH = HC
<=> Tam giác BAC có đường trung tuyến BH bằng 1 nửa cạnh AC.
<=> Tam giác ABC vuông tại B.
mà tam giác BAC cân tại B.
=> Tam giác BAC vuông cân tại B.
Vậy BHCD là hình vuông khi tam giác BAC vuông cân tại B.
KV
31 tháng 10 2023
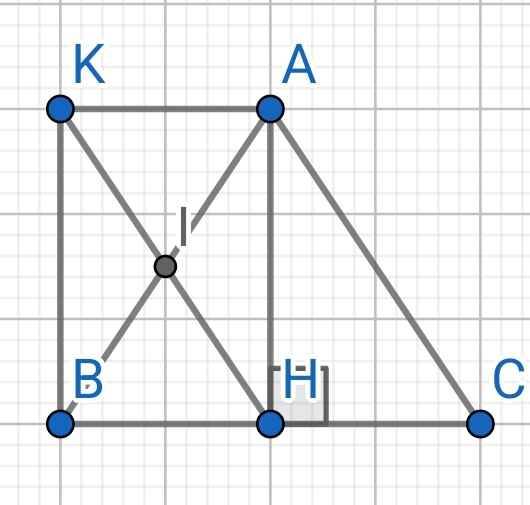a) Do H và K đối xứng nhau qua I
⇒ I là trung điểm của HK
Do AH là đường cao của ∆ABC
⇒ AH ⊥ BC
⇒ ∠AHB = 90⁰
Tứ giác AHBK có:
I là trung điểm HK (cmt)
I là trung điểm AB (gt)
⇒ AHBK là hình bình hành
Mà ∠AHB = 90⁰ (cmt)
⇒ AHBK là hình chữ nhật
b) ∆ABC cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm BC
Mà I là trung điểm AB (gt)
⇒ HI là đường trung bình của ∆ABC
⇒ HI // AC
Tứ giác ACHI có:
HI // AC (cmt)
⇒ ACHI là hình thang
c) ∆ABC đều
⇒ ∠BAC = ∠ACB = 60⁰
⇒ ∠IAC = ∠ACH = 60⁰
Mà ACHI là hình thang (cmt)
⇒ ACHI là hình thang cân
8 tháng 3 2020
https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!
a) Do \(\Delta ABH\)vuông (gt):
mà I Trung điểm AB (gt)
nên \(HI=\frac{1}{2}AB=\frac{6}{2}=3cm\)
b) Xét Tứ giác AHBK:
HI = HK (gt)
AI = AB (gt)
=> Tứ giác ABHK là hình bình hành (2 đường chéo cắt nhau tai trung điểm mỗi đường)
mà \(HI=\frac{1}{2}AB\Leftrightarrow2HI=AB\Leftrightarrow HK=AB\)
=> Hình bình hành ABHK là hình chữ nhật (đpcm).
c) Điều kiện để HCN ABHK là hình vuông thì \(\Delta ABC\)thì:
Dường cao AH = HB
=> HCN AHBK là hình vuông.
ai chịch nhau với mình không