2. chứng tỏ rằng số a= 10 mũ 2011+ 2 mũ3/ 9 là số tự nhiên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 6 2016
=> 102011 + 8 chia hết cho 9
102011+8 = 10000..000+8 (có 2011 số 0)
102011 + 8 = 10000....0008 (có 2010 chữ số 0 )
Vì 1 + 0 + +...+0+8 = 9 nên chia hết cho 9
Vậy a chia hết cho 9 và là số tụ nhiên
NV
4
21 tháng 7 2017
Ta có \(10^{2011}=\left(9+1\right)^{2011}\)Có cùng số dư 12011 = 1 khi chia cho 9
Hay \(10^{2011}\) chia 9 dư 1
Mà 23 = 8 chia 9 dư 8 nên \(10^{2011}+2^3⋮9\)
Hay \(A=\frac{10^{2011}+2^3}{9}\) là số tự nhiên (đpcm)
21 tháng 7 2017
Ta có: \(10^{2011}+2^3=100...0+8\) ( 2011 chữ số 0)
=100...08 ( 2010 chữ số 0)
Tổng các chữ số là: 1+0+0+..+0+8 = 9 ( 2010 chữ số 0) chia hết cho 9
Vậy a là số tự nhiên.
nhớ k!
NM
2
RM
20 tháng 6 2016
Ta có: \(10^{2011}=100...000\) (2011 chứ số 0)
Và \(2^3=8\)
\(\Rightarrow10^{2011}+2^3=100...08\)(2010 chữ số 0)
Số \(100...08\) có tổng các chữ số là: \(1+0+8=9\)(chữ số)
\(\Rightarrow100...08\) chia hết cho 9
Vậy \(a=\frac{10^{2011}+2^3}{9}\) là số tự nhiên.
AC
5
24 tháng 7 2015
\(a=\frac{10^{2011}+2^3}{9}\)
=> 102011 + 8 chia hết cho 9
102011+8 = 10000..000+8 (có 2011 số 0)
102011 + 8 = 10000....0008 (có 2010 chữ số 0 )
Vì 1 + 0 + +...+0+8 = 9 nên chia hết cho 9
Vậy a chia hết cho 9 và là số tụ nhiên
PT
0
13 tháng 7 2023
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
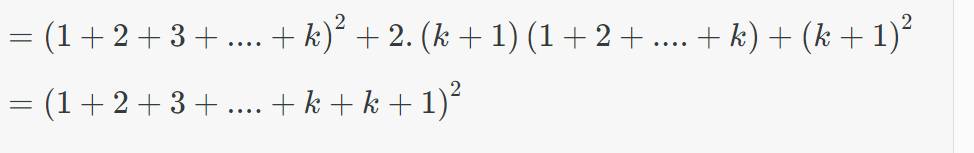
=>ĐPCM
L
7
20 tháng 7 2016
Ta có:
102011 + 23 = 1000...0 + 8 = 1000...08
(2011 chữ số 0)(2010 chữ số 0)
=> tổng các chữ số của 102011 + 23 là: 1 + 0 + 0 + 0 + ... + 0 + 8 = 9 chia hết cho 9
2010 số 0
=> 102011 + 23 chia hết cho 9
Chứng tỏ \(\frac{10^{2011}+2^3}{9}\)là số nguyên
20 tháng 7 2016
Để \(\frac{10^{2011}+2^3}{9}\in N\)thì \(10^{2011}+2^3\) chia hết cho 9
Ta có:102011+23=1000000..........000+8=10000........00008
2011 số 0 2010 số 0
Có tổng các chữ số là:1+0+0+0+............+0+0+0+8=9 chia hết cho 9
2010 số 0
\(\Rightarrow10^{2011}+2^3\) chia hết cho 9
\(\Rightarrow\frac{10^{2011}+2^3}{9}\) là số tự nhiên
DT
2
10 tháng 7 2016
a= (102011+23)/9
Ta có: 10 đồng dư 1 (mod 9) => 102011 đồng dư 12011 (mod 9)
=> 102011 đồng dư 1 (mod 9)
=> 102011+23 đồng dư 1+23 (mod 9) => 102011+23 chia hết cho 9
=> a là số tự nhiên (vì cả tử và mẫu đều dương)