\(\text{\dfrac{3}{4}+ x ×}\dfrac{3}{2}=2\)
MN giải gúp mình với. Cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LD
1
Những câu hỏi liên quan
KH
8 tháng 5 2021
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
TM
8 tháng 5 2021
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....
8 tháng 3 2022
\(C=\dfrac{-5}{7}+\dfrac{-2}{7}+\dfrac{3}{4}+\dfrac{1}{4}+\dfrac{-1}{5}=-1+1-\dfrac{1}{5}=\dfrac{-1}{5}\)
3 tháng 9 2023
1) đkxđ \(\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\y\ge0\end{matrix}\right.\)
Xét biểu thức \(P=x^3+y^3+7xy\left(x+y\right)\)
\(P=\left(x+y\right)^3+4xy\left(x+y\right)\)
\(P\ge4\sqrt{xy}\left(x+y\right)^2\)
Ta sẽ chứng minh \(4\sqrt{xy}\left(x+y\right)^2\ge8xy\sqrt{2\left(x^2+y^2\right)}\) (*)
Thật vậy, (*)
\(\Leftrightarrow\left(x+y\right)^2\ge2\sqrt{2xy\left(x^2+y^2\right)}\)
\(\Leftrightarrow\left(x+y\right)^4\ge8xy\left(x^2+y^2\right)\)
\(\Leftrightarrow x^4+y^4+6x^2y^2\ge4xy\left(x^2+y^2\right)\) (**)
Áp dụng BĐT Cô-si, ta được:
VT(**) \(=\left(x^2+y^2\right)^2+4x^2y^2\ge4xy\left(x^2+y^2\right)\)\(=\) VP(**)
Vậy (**) đúng \(\Rightarrowđpcm\). Do đó, để đẳng thức xảy ra thì \(x=y\).
Thế vào pt đầu tiên, ta được \(\sqrt{2x-3}-\sqrt{x}=2x-6\)
\(\Leftrightarrow\dfrac{x-3}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}=2\end{matrix}\right.\)
Rõ ràng với \(x\ge\dfrac{3}{2}\) thì \(\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}\le\dfrac{1}{\sqrt{\dfrac{2.3}{2}-3}+\sqrt{\dfrac{3}{2}}}< 2\) nên ta chỉ xét TH \(x=3\Rightarrow y=3\) (nhận)
Vậy hệ pt đã cho có nghiệm duy nhất \(\left(x;y\right)=\left(3;3\right)\)
14 tháng 12 2021
\(a,=\dfrac{x^3-\left(x-1\right)\left(x^2+x+1\right)}{1-x}=\dfrac{x^3-x^3+1}{1-x}=\dfrac{1}{1-x}\\ b,=\dfrac{2x+x^2+3x+2+2-x}{\left(x+2\right)^2}=\dfrac{\left(x+2\right)^2}{\left(x+2\right)^2}=1\)
HD
26 tháng 7 2021
Bài 2
b, `\sqrt{3x^2}=x+2` ĐKXĐ : `x>=0`
`=>(\sqrt{3x^2})^2=(x+2)^2`
`=>3x^2=x^2+4x+4`
`=>3x^2-x^2-4x-4=0`
`=>2x^2-4x-4=0`
`=>x^2-2x-2=0`
`=>(x^2-2x+1)-3=0`
`=>(x-1)^2=3`
`=>(x-1)^2=(\pm \sqrt{3})^2`
`=>` $\left[\begin{matrix} x-1=\sqrt{3}\\ x-1=-\sqrt{3}\end{matrix}\right.$
`=>` $\left[\begin{matrix} x=1+\sqrt{3}\\ x=1-\sqrt{3}\end{matrix}\right.$
Vậy `S={1+\sqrt{3};1-\sqrt{3}}`
18 tháng 6 2023
=>9x+4y=360 và 36/x-36/y=1/2
=>4y=360-9x và 36/x-36/y=1/2
=>y=90-2,25x và \(\dfrac{36}{x}-\dfrac{36}{90-2,25x}=\dfrac{1}{2}\)
=>\(\dfrac{3240-81x-36x}{x\left(90-2,25x\right)}=\dfrac{1}{2}\)
=>90x-2,25x^2=2(3240-117x)
=>-2,25x^2+90x-6840+234x=0
=>x=118,3 hoặc x=25,7
=>y=-176,175 hoặc y=32,175
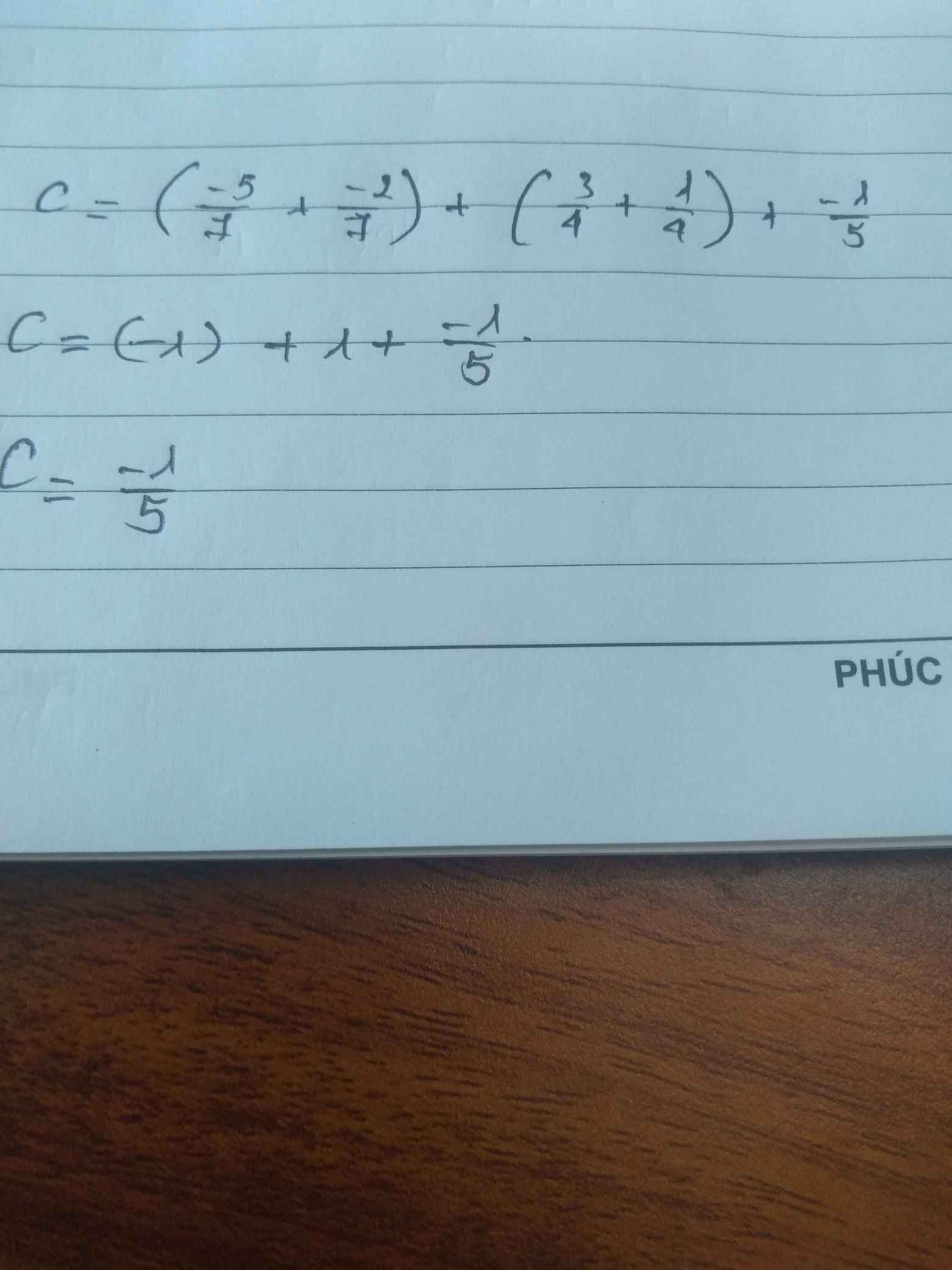
lỗi phép tính r nha e