Question

[Sennn]

giúp em với em cảm ơn nhiều ạ

Answer 1

[Nguyễn Việt Lâm]

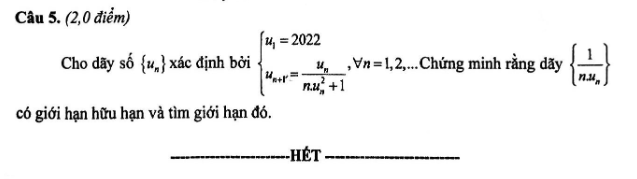
\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)

Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)

Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)

Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng) 

Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\) 

Ta cần chứng minh \(v_{k+1}\ge k+1\)

Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)

Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)

Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)

Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)

Giả sử \(v_k\le k+v_2\)

 \(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)

\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)

Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)