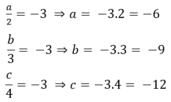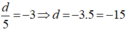Tìm các số a, b, c biết a+b+c =5 và a,b,c # 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.Giải:
Theo bài ra ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{d}{5}\) và a + b + c + d = -42
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{d}{5}=\frac{a+b+c+d}{2+3+4+5}=\frac{-42}{14}=-3\)
+) \(\frac{a}{2}=-3\Rightarrow a=-6\)
+) \(\frac{b}{3}=-3\Rightarrow b=-9\)
+) \(\frac{c}{4}=-3\Rightarrow c=-12\)
+) \(\frac{d}{5}=-3\Rightarrow d=-15\)
Vậy a = -6
b = -9
c = -12
d = -15
Bài 3:
Ta có:\(\frac{a}{2}=\frac{b}{3}\Leftrightarrow\frac{a}{10}=\frac{b}{15}\); \(\frac{b}{5}=\frac{c}{4}\Leftrightarrow\frac{b}{15}=\frac{c}{12}\)
\(\Rightarrow\frac{a}{10}=\frac{b}{15}=\frac{c}{12}\)
Áp dụng tc dãy tỉ:
\(\frac{a}{10}=\frac{b}{15}=\frac{c}{20}=\frac{a+b+c}{10+15+12}=\frac{-49}{37}\)
Với \(\frac{a}{10}=\frac{-49}{37}\Rightarrow a=10\cdot\frac{-49}{37}=\frac{-490}{37}\)
Với \(\frac{b}{15}=\frac{-49}{37}\Rightarrow b=15\cdot\frac{-49}{37}=\frac{-735}{37}\)
Với \(\frac{c}{12}=\frac{-49}{37}\Rightarrow c=12\cdot\frac{-49}{37}=\frac{-588}{37}\)

a:b:c=3:5:7=>a/3=b/5=c/7
Áp dụng t/c dãy tỉ số = nhau:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{10}{15}=\frac{2}{3}\)
=>a=2/3.3=2
b=2/3.5=10/3
c=2/3.7=14/3
Vì a:b:c=3:5:7
=>\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{10}{15}=\frac{2}{3}\)
=>\(\frac{a}{3}=\frac{2}{3}\)=>a=2
\(\frac{b}{5}=\frac{2}{3}\)=>\(b=\frac{10}{3}\)
\(\frac{c}{7}=\frac{2}{3}\)=>\(c=\frac{14}{3}\)


Giải:
Ta có: \(\frac{a}{\frac{b}{c}}=\frac{3}{\frac{5}{7}}\Rightarrow\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b-c}{3-5+7}=\frac{10}{5}=2\)
+) \(\frac{a}{3}=2\Rightarrow a=6\)
+) \(\frac{b}{5}=2\Rightarrow b=10\)
+) \(\frac{c}{7}=2\Rightarrow c=14\)
Vậy a = 6, b = 10, c = 14

Đặt : \(\frac{a}{5}=\frac{b}{3}=\frac{c}{7}=k\Rightarrow\hept{\begin{cases}a=5k\\b=3k\\c=7k\end{cases}}\)
=> \(a-b+c=36\)
=> \(5k-3k+7k=36\)
=> \(9k=36\)
=> \(k=4\)
Với k = 4 thì \(\hept{\begin{cases}a=5k=5\cdot4=20\\b=3k=3\cdot4=12\\c=7k=7\cdot4=28\end{cases}}\)
P/S : Lớp 6 đã học cái này rồi à ?

Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{-5}=\frac{b}{-7}=\frac{c}{2}=\frac{a-b+c}{-5+7+2}=-\frac{28}{4}=-7\)
\(\Rightarrow a=35;b=49;c=-14\)
Trả lời:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{-5}=\frac{b}{-7}=\frac{c}{2}\)\(=\frac{a-b+c}{-5-\left(-7\right)+2}=\frac{-28}{4}=-7\)
\(\Rightarrow\hept{\begin{cases}a=-7.\left(-5\right)=35\\b=-7.\left(-7\right)=49\\c=-7.2=-14\end{cases}}\)
Vậy a = 35; b = 49; c = - 14

\(\frac{a}{2}=\frac{b}{3};\frac{b}{5}=\frac{c}{4}\)
\(\Rightarrow\frac{a}{10}=\frac{b}{15}=\frac{c}{12}=\frac{a-b+c}{10-15+12}=-\frac{49}{7}=-7\)
\(\frac{a}{10}=-7\Rightarrow a=-70\)
\(\frac{b}{15}=-7\Rightarrow b=-105\)
\(\frac{c}{12}=-7\Rightarrow c=-84\)
tíc mình nha

Ta có: a : b : c : d = 2 : 3 : 4 :5 và a + b + c + d = -42
Suy ra:
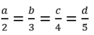
Theo tính chất dãy tỉ số bằng nhau ta có;
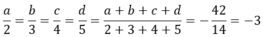
Ta có: