Cho tam giác ABC có AB = 15cm, BC = 70cm, CA = 65cm. Biết \Delta ABC\sim\Delta A'B'C'ΔABC∼ΔA′B′C′ và chu vi tam giác A'B'C' là 90cm. Tính độ dài các cạnh của tam giác A'B'C'.
A'B' = cm.
B'C' = cm.
C'A' = cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm
14 tháng 4 2020
AB = 18; BC = 21; CA =12 (gt)
=> chu vi tg ABC là : 18 + 12 + 21 = 51
tam giác ABC ~ tam giác A'B'C' (gt)
=> AB/A'B' = AC/A'C' = BC/B'C' = C ABC/C A'B'C
=> AB/A'B' = AC/C'A' = BC/B'C' = 3/4
xong tự tính ra
27 tháng 1 2022
a: \(\text{Δ}ABC\sim\text{Δ}HBA;\text{Δ}ABC\sim\text{Δ}HCA\)
b: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
CH=BC-BH=25-9=16(cm)
P
17 tháng 3 2018
a, ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{4}{12}=\dfrac{5}{15}=\dfrac{1}{3}\)
=> DE//BC
vì DE//BC => tam giác ADE đồng dạng tam giác ADC
b, ta có EC= 15-5=10
BD= 12-4=8
vì EF//AB
=> \(\dfrac{EC}{AC}=\dfrac{EF}{AB}=\dfrac{10}{15}=\dfrac{EF}{12}\)
=> EF=(10.12):15=8
=> EF=BD
Xét tứ giác BDEF có:
EF=BD
EF//BD (vì EF//AB)
=> BDEF là hình bình hành
c,Vì BDEF là hình bình hành
=> DE=BF
mà \(\dfrac{DE}{BC}=\dfrac{AD}{AB}=\dfrac{DE}{18}=\dfrac{4}{12}\) (DE//BC)
=> DE=BF= (18.4):12=6
=>FC= 18-6=12
PT
16 tháng 4 2023
Bạn tự vẽ hình nhé^^
a) xét tam giác HDC và tam giác HEB có:
góc E= góc D(=90 độ)
góc EHB = góc DHC(2 góc đối đỉnh)
=> tam giác HDC đồng dạng tam giác HEB(g-g)
=>HD/HE = HC/HB=> HD.HB=HE.HC(đpcm)
b)Xét tam giác ADB vuông tại D và tam giác AEC Vuông tại E có:
góc A: góc chung
=> tam giác ADB đồng dạng tam giác AEC (g-g)
=>AD/AE=AB/AC
Xét tam giác AED và tam giác ACB có:
góc A: góc chung
AD/AE=AB/AC (cmt)
=> tam giác AED đồng dạng tam giác ACB(c-g-c)
=>góc ADE=góc ABC (đpcm)
17 tháng 4 2023
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
chung
Do đó: ΔABDΔACE(g-g)
b) Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
(hai góc đối đỉnh)
Do đó: ΔHEBΔHDC(g-g)
Suy ra:
hay
22 tháng 5 2018
a) Xét tam giác AHN và tam giác ACH có :
Góc AHC chung
Góc ANH = Góc AHC ( = 90oC)
⇒ Tam giác AHN ~ tam giác ACH ( TH3)
b) Áp dụng định lý Py-ta-go vào tam giác ABH có :
BH2 = AB2 - AH2
BH = \(\sqrt{AB^2-AH^2}\)
BH = 9 ( BH > 0)
Tương tự , ta có : HC = 5 ( cm)
⇒ BC = BH + HC = 9 + 5 = 14 ( cm)
c) Ta có : tam giác AHN ~ Tam giác ACH ( TH3 )( Câu a)
⇒ \(\dfrac{AH}{AC}=\dfrac{AN}{AH}\)
⇒ AH2 = AN.AC ( 1)
Cmtt câu a) Tam giác AMH ~ Tam giác AHB
⇒ \(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
⇒ AH2 = AM.AB ( 2)
Từ ( 1 ; 2) ⇒ AN.AC = AM.AB
⇒ \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)
Xét tam giác AMN và tam giác ACB có :
Góc BAC chung
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\) ( cmt)
⇒ Tam giác AMN ~ Tam giác ACB ( TH2 )
d) Theo CM câu c) Ta có : \(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
⇒ AM = \(\dfrac{AH^2}{AB}=\dfrac{48}{5}=9,6\left(cm\right)\)
Theo câu c) Lại có : Tam giác AMN ~ Tam giác ACB ( TH2)
⇒ \(\dfrac{AM}{AC}=\dfrac{MN}{BC}\)
⇒ MN = \(\dfrac{AM.BC}{AC}=\dfrac{9,6.14}{13}=10,34\left(cm\right)\)
22 tháng 5 2018
a) xét tam giac ahn và tam giác ach có
góc ahc = góc anh=90 độ
góc a chung
suy ra ta có tam giac ahn đồng dạng với tam giác ach(g.g)
17 tháng 9 2023
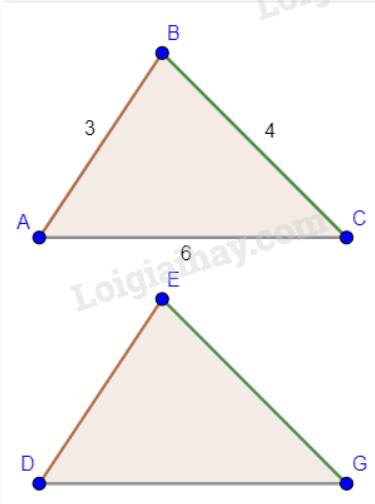
\(\Delta ABC = \Delta DEG\) nên AB = DE, BC = EG, CA = GD.
Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\)cm,\(EG = 4\)cm,\(GD = 6\)cm.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm