Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm

AB+BC+AC=18cm
nên AC=6cm
AB/A'B'=AC/A'C'=BC/B'C'=2
=>4/A'B'=6/A'C'=8/B'C'=2
=>A'B'=2; A'C'=3; B'C'=4

ΔABC~ΔA'B'C'
=>\(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
=>\(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\)
=>AB là cạnh nhỏ nhất trong ΔABC
Theo đề, ta có: AB=3cm
=>\(\dfrac{AC}{4}=\dfrac{BC}{5}=\dfrac{3}{3}=1\)
=>\(AC=4\cdot1=4\left(cm\right);BC=5\cdot1=5\left(cm\right)\)

a: Xét ΔA'B'C' và ΔABC có
A'B'/AB=A'C'/AC=B'C'/BC
Do đó: ΔA'B'C'\(\sim\)ΔABC
b: \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{A'B'}{AB}=2\)

Vì ∆ A’B’C’ đồng dạng với tam giác ABC nên A′B′AB=A′C′AC=B′C′BCA′B′AB=A′C′AC=B′C′BC (1)
Thay AB = 3(cm), AC = 7 (cm), BC = 5 (cm) , A’B’ = 4,5 (cm) vào (1)
ta có: 4,5/3=A′C′/7=B′C′/5 (cm)
Vậy: A’C’ =7.4,5/3=10,5=7.4,53=10,5 (cm)
B’C’ =5.4,5/3=7,5 (cm).
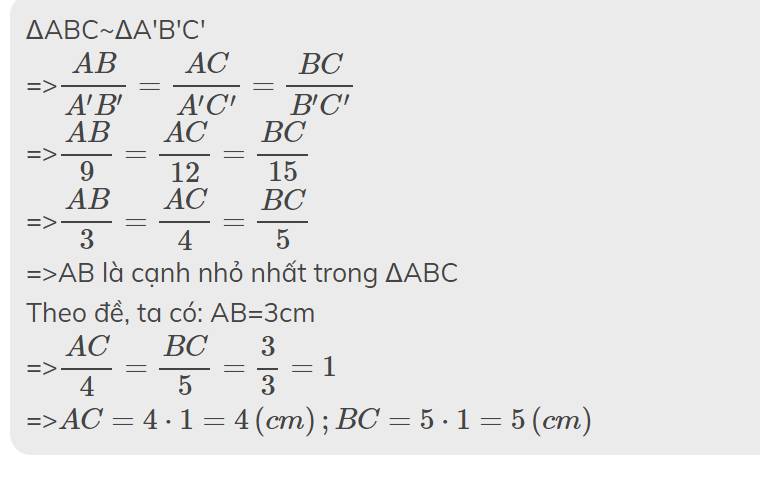
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm