Một hỗn hợp X gồm FeSO4 và Al2(SO4)3,trong đó số ngyên tử oxi trong X chiếm 20/29 tổng số nguyên tử trong các nguyên tố trong hỗn hợp X. Tính thành phàn % khỗi lượng mỗi chất trong hỗn hợp X.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2021
Đặt tỉ lệ số phân tử Fe2(SO4)3 và MgSO4 là x,y
=> Số nguyên tử O: 12x + 4y
Tổng số nguyên tử: 17x +6y
Ta có:
\(\dfrac{12x+4y}{17x+6y}=\dfrac{32}{47}\Leftrightarrow47.\left(12x+4y\right)=32.\left(17x+6y\right)\\ \Leftrightarrow564x-544x=192y-188y\\ \Leftrightarrow20x=4y\\ \Leftrightarrow\dfrac{x}{y}=\dfrac{1}{5}\)
=> Phần trăm khối lượng mỗi chất trong hh:
\(\%mFe2\left(SO4\right)3=\dfrac{400.1}{400.1+120.5}.100=40\%\\ \%mMgSO4=100\%-40\%=60\%\)
17 tháng 7 2018
Đáp án C
Gọi
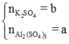
Áp dụng định luật bảo toàn nguyên tố cho O, Al, K và S ta có:
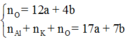
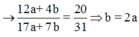
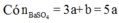
Nên
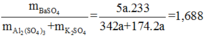
Đáp án C
26 tháng 6 2017
Đáp án : D
Giả sử có 1 mol hỗn hợp gồm x mol Al2(SO4)3 và (1 – x) mol K2SO4
=> tổng số mol các nguyên tố
= nAl + nK + nS + nO = 2x + 2.(1 – x) + (3x + 1 – x) + 4.( 3x + 1 – x) = 10x + 7
=>nO = nngto.%nO
=> 4.(3x + 1 – x) = (10x + 7).20/31
=> x = 1/3 mol
=> mhh đầu = 230g
Khi phản ứng với BaCl2 thì nBaSO4 = nSO4 = 3x + 1 – x = 5/3 mol
=> mBaSO4 = 388,3g
=> mBaSO4 : mhh = 1,688 lần
6 tháng 2 2022
Gọi số nguyên tử của \(Al_2(SO_4)_3\) và \(K_2SO_4\) lần lượt là x và y.
Số nguyên tử của \(Al_2(SO_4)_3\) là \(2+3+4\cdot3=17x\)
Số nguyên tử của \(K_2SO_4\) là \(2+1+4=7y\)
Mà số nguyên tử \(O_2\) trong hỗn hợp là \(4\cdot3x+4y=12x+4y\)
Theo bài: \(n_{O_2}=\dfrac{20}{31}n_{hh}\)
\(\Rightarrow12x+4y=\dfrac{20}{31}\left(17x+7y\right)\)
\(\Rightarrow y=2x\)
Có \(\%m_{Al_2\left(SO_4\right)_3}=\dfrac{342x}{342x+174y}\cdot100\%=\dfrac{342x}{342x+174\cdot2x}\cdot100\%=49,56\%\)
\(\%m_{K_2SO_4}=100\%-49,56\%=50,44\%\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
6 tháng 2 2022
\(\%m_{\dfrac{O}{Nhôm.sunfat}}=\dfrac{4.16.3}{342}.100\approx56,14\%\\ \%m_{\dfrac{O}{Kali.sunfat}}=\dfrac{4.16}{174}.100\approx36,78\%\\ Gọi:a=n_{Al_2\left(SO_4\right)_3};b=n_{K_2SO_4}\left(a,b>0\right)\\ \Rightarrow Vì:m_{\dfrac{O}{hh}}=\dfrac{20}{31}\\ \Leftrightarrow\dfrac{a.12+b.4}{17a+7b}.100\%=\dfrac{20}{31}\\ \Leftrightarrow32a=16b\\ \Leftrightarrow\dfrac{a}{b}=\dfrac{16}{32}=\dfrac{1}{2}\\ \Leftrightarrow b=2a\\ \%m_{\dfrac{K_2SO_4}{hh}}=\dfrac{174.2a}{174.2a+342.a}.100\%\approx50,435\%\\ \Rightarrow\%m_{\dfrac{Al_2\left(SO_4\right)_3}{hh}}\approx49,565\%\)
27 tháng 3 2023
Gọi: \(\left\{{}\begin{matrix}n_{Al_2\left(SO_4\right)_3}=x\left(mol\right)\\n_{CuSO_4}=y\left(mol\right)\end{matrix}\right.\) ⇒ mhh = 342x + 160y (g)
BTNT O, có: \(n_O=12n_{Al_2\left(SO_4\right)_3}+4n_{CuSO_4}=12x+4y\left(mol\right)\)
⇒ mO = 16.(12x+4y) = 192x + 64y (g)
Mà: O chiếm 48,34% khối lượng.
\(\Rightarrow\dfrac{192x+64y}{342x+160y}=0,4834\) \(\Rightarrow y=2x\)
\(\Rightarrow\%m_{Al_2\left(SO_4\right)_3}=\dfrac{342x}{342x+160y}.100\%=\dfrac{342x}{342x+160.2x}.100\%\approx51,66\%\)
\(\%m_{CuSO_4}\approx48,34\%\)
21 tháng 3 2023
Gọi: \(\left\{{}\begin{matrix}n_{Al_2\left(SO_4\right)_3}=a\left(mol\right)\\n_{Na_2SO_4}=b\left(mol\right)\end{matrix}\right.\) \(\Rightarrow m_X=342a+142b\left(g\right)\)
BTNT O, có: \(n_O=12n_{Al_2\left(SO_4\right)_3}+4n_{Na_2SO_4}=12a+4b\left(mol\right)\)
\(\Rightarrow m_O=16.\left(12a+4b\right)=192a+64b\left(g\right)\)
Mà: O chiếm 50% về khối lượng.
\(\Rightarrow\dfrac{192a+64b}{342a+142b}=0,5\) \(\Rightarrow b=3a\)
\(\Rightarrow\%m_{Al_2\left(SO_4\right)_3}=\dfrac{342a}{342a+142b}.100\%=\dfrac{342a}{342a+142.3a}.100\%=44,53125\%\)
\(\%m_{Na_2SO_4}=100-44,53125=55,46875\%\)
3 tháng 10 2016
Đầu tiên anh không ngờ là e lại chịu khó cày đến như vậy. Anh sẽ hướng dẫn e làm bài này:
gọi số mol nhôm sunfat là x, kali sunfat là y
trong nhôm sunfat có 17 nguyên tử, trong đó có 12 nt oxi
trong kali sunfat có 7 nt, trong đó có 4 nt oxi
đến đây e lập tỷ lệ: ====>2x-y=0
sau đó e giả sử hỗn hợp ban đầu là 3 mol( e lấy bnhiu kug dc, a lấy 3 mol vì nó ra số chẵn), ta có thêm 1 pt nữa: x+y=3
Giải hệ này e dc : x=1: y=2
tỷ lệ em cần tìm là:
Gọi số mol FeSO4, Al2(SO4)3 là a, b (mol)
nFe = a (mol)
nAl = 2b (mol)
nS = a + 3b (mol)
nO = 4a + 12b (mol)
Có: \(\dfrac{n_O}{\Sigma n}=\dfrac{4a+12b}{a+2b+a+3b+4a+12b}=\dfrac{20}{29}\)
=> a = 2b
\(\left\{{}\begin{matrix}\%m_{FeSO_4}=\dfrac{152a}{152a+342b}.100\%=\dfrac{152.2b}{152.2b+342b}.100\%=47,059\%\\\%m_{Al_2\left(SO_4\right)_3}=100\%-47,059\%=52,941\%\end{matrix}\right.\)