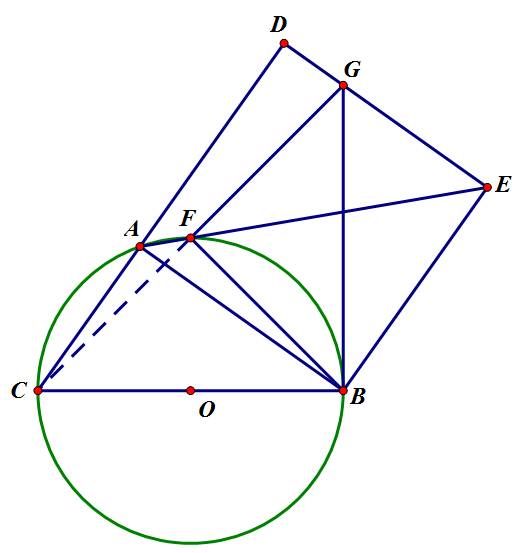
Cho đường tròn tâm O, đường kính BC, A nằm trên cung BC. Trên AC lấy D sao cho AB = AD. Dựng hình vuông ABED, AE cắt đường tròn tâm O tại F, tiếp tuyến tại B cắt DE tại G
a. Chứng minh tứ giác BGDC nội tiếp và xác định tâm Y của đường tròn
b. Chứng minh: tam giác BFC vuông cân, F là tâm đường tròn ngoại tiếp tam giác BCD
c. Chứng minh tứ giác GEFB nội tiếp