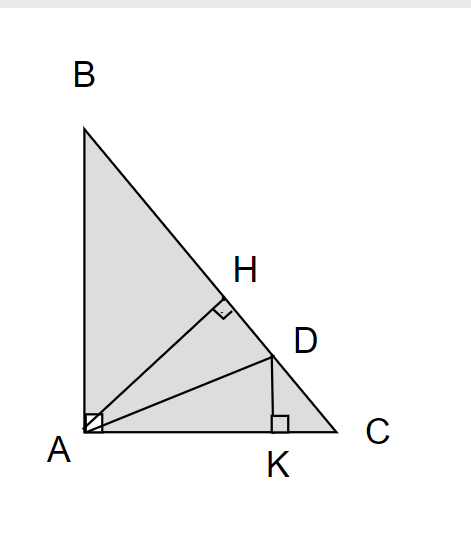
Cho tam giác ABc vuông tại A .vẽ đường cao AH . Trên cạnh BC lấy điểm D sao cho BD=BA
a/ Chứng minh :góc BAD=góc ADB
b/ chứng minh : AD là phân giác của góc HAC
c/ Vẽ DK vuông góc với AC [K thuộc AC] .c/m :Ak=AH
d/ Chứng minh : AB+AC<BC+2AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2022
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
YP
11 tháng 5 2022
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
28 tháng 7 2023
a: BA=BD
=>ΔBAD cân tại B
=>góc BAD=góc BDA
b: góc HAD+góc BDA=90 độ
góc CAD+góc BAD=90 độ
mà góc BAD=góc BDA
nên góc HAD=góc CAD
=>AD là phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔADH=ΔADK
=>AH=AK
YN
28 tháng 7 2023
bài giải nè ! 
a: BA=BD
=>ΔBAD cân tại B
=>góc BAD=góc BDA
b: góc HAD+góc BDA=90 độ
góc CAD+góc BAD=90 độ
mà góc BAD=góc BDA
nên góc HAD=góc CAD
=>AD là phân giác của góc HAC
c: Xét ΔADH vuông tại H và ΔADK vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔADH=ΔADK
=>AH=AK
HP
27 tháng 4 2016
hình tự vẽ
a)Vì BD=BA (gt)
=>\(\Delta ABD\) cân ở B (DHNB)
=>góc BAD = góc ADB (t/c tam giác cân)
b)Ta có: góc BDA là góc ngoài của \(\Delta ACD\)
=>góc BDA = \(\)góc ACD + góc DAC (1)
góc DAB=góc DAH + góc HAB (2)
Mà góc ABC + góc ACB = 900 (t/c tam giác vuông)
=>góc ACB = 900 - góc ABC
góc HAB + góc ABC = 900(t/c tam giác vuông)
=>góc HAB = 900 - góc ABC
=>góc ACB = góc HAB (3)
Từ (1);(2);(3);có góc BAD = góc BDA (cmt)
=>góc KAD = góc HAD ,mà AD nằm giữa AK và AH
=>AD là tpg của góc HAC (=góc KAH)
c)Xét \(\Delta AKD\) vuông tại K và \(\Delta AHD\) vuông tại H có:
AD:cạnh chung
góc KAD = góc HAD (cmt)
=>\(\Delta AKD=\Delta AHD\left(ch-gn\right)\)
=>AH=AK (cặp cạnh tương ứng)
d)Xét \(\Delta AHB\) vuông tại H có:
AH + HB > AB (BĐT tam giác) (4)
Xét \(\Delta AHC\) vuông tại H có;
AH + HC > AC (BĐT tam giác) (5)
Cộng (4) và (5),vế theo vế ta đc:
AH + HB + AH + HC > AB + AC
=>AB + AC < BC + 2AH (đpcm)