Cho hình vuông ABCD.Gọi I là một điểm nằm giữa A và B.Tia DI và tia CB cắt nhau ở K.Kẻ đường thẳng qua D,vuông góc với DI,đường thẳng này cắt đường thẳng BC tại L.Chứng minh rằng:a) Tam giác DIL là tam giác cân;b)Tổng \(\frac{1}{DI^2}\)+ \(\frac{1}{DK^2}\)không đổi khi I thay đổi trên cạnh...
Đọc tiếp
Cho hình vuông ABCD.Gọi I là một điểm nằm giữa A và B.Tia DI và tia CB cắt nhau ở K.Kẻ đường thẳng qua D,vuông góc với DI,đường thẳng này cắt đường thẳng BC tại L.Chứng minh rằng:
a) Tam giác DIL là tam giác cân;
b)Tổng \(\frac{1}{DI^2}\)+ \(\frac{1}{DK^2}\)không đổi khi I thay đổi trên cạnh AB
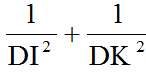
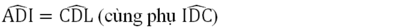
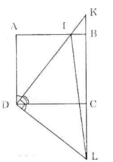
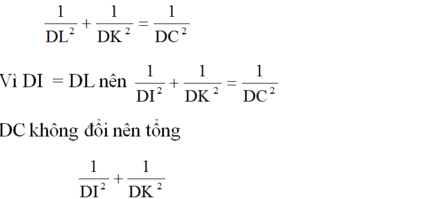
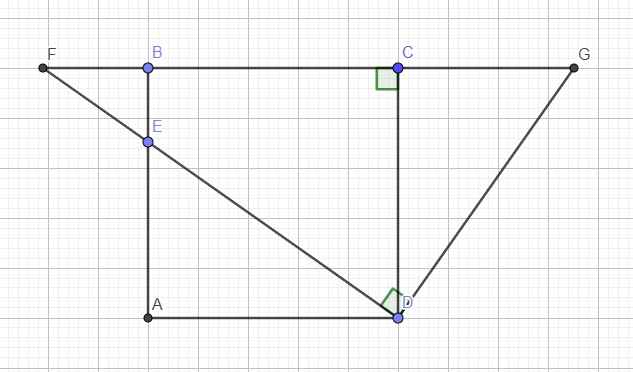
đặt góc IAD là D1; góc IDC là D2; góc CDL là D3
a) Ta có D1+D2=90độ
D2+D3=90độ
=>D1=D3
xét 2tam giác vuông IAD và DCL
Có D1=D3(CM trên)
AD=DC(cạnh hình vuông)
=> tam giác IAD=tam giác LCD(góc nhọn-cạnh góc vuông)
=>DL=DI
=> tam giác IDL cân tại D
b) xét tam giác vuông KDL có
DC là đường cao
=> 1/DC^2=(1/DK^2)+(1/DL^2) (1)
Mà DL=DI (2)
mà DC không đổi (3)
Từ (1),(2) và (3) =>DPCM