Giúp pé với🥲
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 10 2023
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=9+144=153\)
=>\(BC=3\sqrt{17}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}=4\)
=>\(\widehat{B}\simeq75^057'\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN\(\sim\)ΔACB
29 tháng 12 2021
14: \(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}=\dfrac{4}{4x+7}\)
TT
1
30 tháng 7 2023
14:
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
13:
a: 3x+5=x-5
=>2x=-10
=>x=-5
b: (x-2)(2x+5)=0
=>x-2=0 hoặc 2x+5=0
=>x=2 hoặc x=-5/2
c: =>2(5x-2)=3(3x+1)
=>10x-4=9x+3
=>x=7
d: =>(3x+6-x+1)/(x+2)(x-1)=17-3x/(x+2)(x-1)
=>2x+7=17-3x
=>5x=10
=>x=2
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
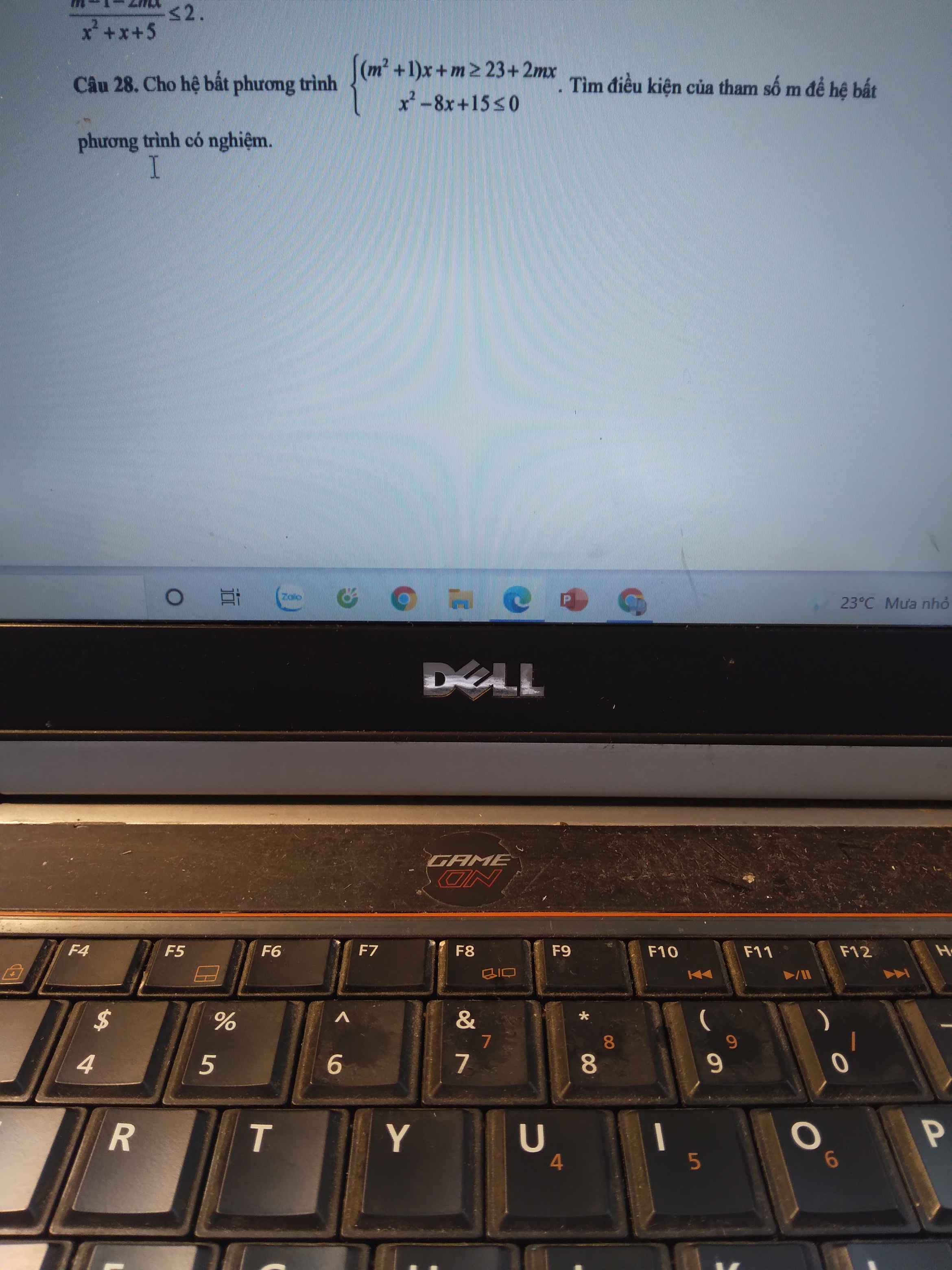
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)
Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)
\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)
\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)
- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)
- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)
\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)
Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)
\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)
\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)
PN
2
KB
28 tháng 3 2022
\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1
Q9
1
pé nào
hông bé ơi :))